2022-12-20

マラソンではじめる効果的なKPT

この記事は Sansan Advent Calendar 2022 20日目の記事です．昨日は id:nersonu さんによる「高速かつ PEP 582 で仮想環境を捨てる Python パッケージマネージャ PDM を試す」でした． PEP582もPDMも知らなかったので勉強になりました．これまでの記事は以下からご覧ください．

adventar.org

はじめに：振り返り
KPTへの課題感と思索
課題への対策
実践：マラソンではじめる効果的なKPT
おわりに

はじめに：振り返り

さて，2022年はどんな1年だったでしょうか．私はというと，苦しいながらも，継続とチャレンジのバランスが取れた1年だったような気がします．

継続では，学生時代からの研究で学会に行ったり論文を出したり，去年から続いているランニングではマラソンに出たりしていました．チャレンジ面では，新しい研究プロジェクトをキックしたり，これまで縁のなかったギターを始めたりしました．

マラソンは，2本のフル (42.195km) と1本のハーフ (21km) に出場しました． 4月に出た長野マラソンでは，初出場にしてサブ4（4時間切り）を達成することができました．これは上位3割ぐらいの成績です．一方，12月に出た青島太平洋マラソンでは，4時間48分もかかってしまいました． 4時間切りは余裕だろうと高を括っていたので，非常に悔しかったです．悔しさのあまり，その夜は焼酎に溺れていました．あまりに悔しいので，雪辱を果たすべくしっかりと振り返りを行い，次に活かしたいと思います．

ところで，振り返りって難しいですよね．何かを改善するための振り返りならば，たくさんの方法が知られています（何かを改善することだけが，振り返りの目的ではないとも思います）．なかでも最も有名なものはKPTでしょうか．私も，業務ではKPTを実施することがしばしばあります．

KPT とは，次の3つのステップで現状を分析するものです．

K：Keep（良かったこと，これからも続けること）
P：Problem（悪かったこと，改善すべきこと）
T：Try（次に試みること）

このフレーム（制限）に従うことで，振り返りのコメントを出しやすくなることや，挙げられたKeepとProblemから自然なTryが考えやすくなることなどのメリットがあるでしょう．また，チームで実施することにより，様々な視点で，合意のとれた次のアクションを取ることなどができます（今回は1人で実施します）．

一方で，個人的には，KPTでの振り返りには漠然とした難しさを感じていました．

このポエムでは，次のレースをより良いタイムで走ることを目的とし，大失敗した青島太平洋マラソンを対象に振り返りを実施したいと思います．またその中で，私が感じているいくつかのKPTの難しさを克服することを試みてみます．

しばしお付き合いください

KPTへの課題感と思索

私が抱いていた課題感（難しさ）を要約してみると，以下のようにまとまりました．

Problemばかり上げてしまう
何についてどの粒度で書くか難しい．結果として幼稚な感想になってしまう
Tryが継続的に実行できているか，計測できていない（建てるだけにしない）

それぞれについて考えてみます．

Problemばかりあげてしまう

Keepが少なくProblemばかりになってしまっているな，という漠然とした感覚がありました．悪いとこばかりに目が行きがちなのかもしれないですね．また，そもそもKeepが少ないことは問題なのか，という自然な疑問があります．

Keepには，「前回までのTryのうち良かったものを拾い上げ継続させる」，「Tryには由来しないが，フワッと始めた手応えのある取り組みをより本格化させる」，などの効果があるはずです．

こういったものを見落としてはもったいないので，Keepを見つけることはたしかに重要そうです．

何についてどの粒度で書くか難しい

おそらくこれが最も問題です．「良いことはなんだったか」「問題はなんだったか」という問い（制限）だけでKeepやProblemを挙げるだけでは，雑多なものになってしまうのは当然かもしれません．

これは私のケースですが，Problemにおいてそもそもの行動が悪かったのか，途中の状態が悪かったのかを混同して書いてしまうことがよくありました．また，客観視できるものと定性的な主観が混ぜてしまってもいました．

もちろん，満遍ない切り口で振り返り発散させることは大切だと思います．しかし，現実的なリソースで効果的なTryを見つけ実施するためには，自分の影響できる範囲とそうでない範囲を見定め，中でも結果に直結しそうなところに介入するのが重要そうです．そのためには，想定される全体のメカニズムの中でどの部分に言及しているのか，またその言及は感想から数値に落とし込めるのかを考えることが良さそうです．

Tryが継続的に実行できているか，計測できていない

いくら良いTryを立てても，適切に実行されなければ意味がありません．そのためには，Tryを実行できているか，その進捗はどうなっているか，継続的に振り返る必要があります．

人間が努力により意識的に行動するのは限界がある，と個人的には考えています．ウィジェットやツールを駆使することも考えられそうですが，そのうち慣れきってしまい効果がなくなると容易に想像されます． 1ヶ月後には，「走る時間です」「目標の月間100kmに対して現在30kmです」のような通知を一瞬でスワイプアウトしているでしょう．

以上より，軽量な振り返りを短く回させざるを得ない状況を用意することが重要そうです．少なくとも，半年に1度しかレースに出ていない現状は不適切といえそうです．

課題への対策

前節で挙げた課題とそれについての思索から，以下のような対策を考えました．

はじめに自分の行動と，それが結果に影響を及ぼすまでのメカニズムを想定する
- このとき，自分の介入できる部分とそうでない部分を切り分ける
想定したメカニズムと睨めっこしながら，定量値と感想を集め，Keep候補 / Problem候補とする．
候補を精査し，Keep / Problem を練る
- メカニズムのどの部分への言及なのか
- 感想はできるだけ定量指標に落とし込む
Tryへと昇華させる
- 想定されるメカニズムのどこに介入すると効果が大きいかを考える
- 環境や運の要素が大きくても，コスト低くできるなら取り入れる
上記一連の振り返りを短期間で実施しなければならない状況を用意する

実践：マラソンではじめる効果的なKPT

それでは，これまで考えたKPTの改善をもとに，大失敗した青島太平洋マラソンを振り返っていきます．

まず，KPTに入っていく前の作業をします．具体的には，振り返りサイクルを回さざるを得ない環境を用意します．そして，マラソンにおいて行動から結果が出るまでのメカニズムを想定します．

振り返りのサイクルを回す状況を用意する

友人とのランニング会を月に1度固定で入れることし，カレンダーを押さえました．
ハーフマラソンに3ヶ月に1度，本番の前3ヶ月は1ヶ月に1度出ることにしました．
- 次は3月の立川シティハーフマラソンです．

行動から，結果が出るまでのメカニズムを想定する

次の図のように整理しました．介入できるものは角のある四角で表しています．

Keep候補

上記メカニズムに立ち返りながら，KeepとProblemの候補になる事象・感想を集めていきます

2本のフルマラソン，1本のハーフマラソンにエントリーした
ハーフマラソンでは自己ベストを更新した（1時間48分）
- 平均心拍数は184
- 足の痛みなどもなかった
年間609km走った
やれる調整はやった
- レース1週間前の距離抑える．強度少し高めとジョグ混ぜる
- カーボローディングした
- カフェイン断ちした
青島太平洋マラソンでは，中間地点までは平均心拍数175程度で巻き返せている
- 一方で，道が狭く，序盤ペースを挙げるのに（人を抜くのに）集中力を使った（Problem）

Problem候補

本番（青島太平洋マラソン）

暑かった（19度，快晴）
足攣った（25km地点）
足が攣る直前，21 ~ 25kmでペースが落ちている→バテ？スタミナ？
12月のフルマラソンで足が攣った
- エネルギーとアミノ酸しか補給していない
前日に飲酒をした
- ビール5本程度，焼酎
- 地鶏，刺身，チキン南蛮，etc
レース後膝痛い．
- 長野マラソンではそこまででなかった．→ 距離が足りない，フォームは問題ない
- 痛みがあるのは靭帯 → 筋肉量が足りない
睡眠時間が足りてない
- 本番前1週間の平均が5時間
- 最近不眠の傾向あり

本番までの練習

夏（1本目のフルマラソン以降）に全く練習していない
- 5~9月の走行距離が40km程度
- いずれも1km6分ペースでの5kmジョグ（ポイント練習の欠如）
秋の走り込みが足りてない
- 月間60 ~ 80kmしか走ってない（長野マラソンの前は100km走れていた）
- 21km以上走った日がない
VO2maxが長野マラソンのときと比べて4低い（心肺機能の低下）
- 夏の全く走らなかった期間の下落が大きい

Keep

Keep候補を精査し，サマります．

21kmまでの対応は現状の練習で問題ない
- 足の状態をみても，カーボンシューズで21kmは耐えれる
継続的にフルマラソンにエントリーしている
巡行できるスピードは上がっている．

Problem

続いてProblem候補を精査し，サマります． Keepを踏まえ，21kmまでは対応できていることや，それ以上の距離に耐える足が作れてないことを考慮しました．

お酒は美味しいので不問とします．睡眠時間が短いのもどうしようもないので諦めます．

ハーフ以上の距離に耐えられる足がない
距離を走らざるを得ない環境が用意できてない
気温（19度，快晴）にやられた
- 暑さや日光の対策をしていない
足攣りの対策をしていない
夏に走り易い環境がない
- 距離は短くて良く，全く走らないことでVO2maxが下がるのが問題

Try

装備

装備で暑さ対策をする（お金に頼る）
- 短パン
- サングラス
- 髪を切る
足攣り対策をする
- マグネシウム入りの補給を試す
後半の集中力を高める
- カフェイン入りの補給も試す
長い距離で厚底シューズを履きこなす
- スピード練習だけでなく長いペース走でも必ずズームフライ4を履く

立川シティハーフに向けた練習

友人と1ヶ月に1度ロング走の予定を入れる
- 毎月最終曜日に設定
長めのペース走を中心にする．
精神負荷をかけない
- 月間100km以上は走らなくて良いことにする
- スピード練習はやる気があるときにやる

ちょっと先の練習

夏に自然と走る体制を作る
- 短期ジムを契約する（6~9月）
- スピード練習と筋トレ，アクティブレストのみに絞り，45分以上は運動しない
秋に距離を走る
- レースの3ヶ月前から，毎月ハーフマラソンにエントリーする
- ハーフマラソンと並行し，ロング走の予定も実施する
- 月間100km以上は走らなくて良いことにする

おわりに

オレオレでKPTを改善し，実践してみました．改善した振り返りが適切であったかどうかは，今後のタイムが証明してくれることでしょう．

明日は sin_chir0 さんです．楽しみですね．

それではごきげんよう

2021-12-19

足を速く"した" 話

こんにちは，kur0cky です．そしてこれは，Sansan Advent Calendar 2021 の19日目の記事です．

【内容を3行で】

the 不健康である私がランニングにハマりハーフマラソンに出た
情報収集して evidence based なトレーニングをしたら目標タイムを軽く上回った
実践に活かした論文を紹介する

長めの前書きと導入
取り組み
- 立てたトレーニング戦略
- 結果
論文紹介（本題）
- 1本目：Aerobic High-Intensity Intervals Improve VO2max More Than Moderate Training (Helgerud et al., 2007)
- 2本目：National Athletic Trainers' Association Position Statement: Prevention of Anterior Cruciate Ligament Injury (Padua et al.,2018)
おわりに
参考文献

長めの前書きと導入

去年のアドベントカレンダーを書いてから，1年間投稿がありません．勉強会に登壇したり会社のブログを書いたりはしていましたが，学生の頃はもっと色々やっていたような気がします．体力に身をまかせるのもそろそろ仕舞いにしないといけないかもしれません．

そんな2021年でしたが，一つ趣味が増えました．ランニングです．これ以上趣味が増えると命を削らないといけません．

思いつき

恥の多い生涯を送ってきました．私には，健康な生活というものが，見当つかないのです．中学の頃には運動部に所属していたこともありました．しかしそれきり，1kmも走ることなく，酒を煽り，泥のように眠り，怠惰な生活に明け暮れていました．動かすのも指先と口先ばかり，私は不健康を体現する人間として次第に完成されていったのです．継続は力です．そこそこにあった筋肉は影も形もなく，夜を徹することもできなくなってきました．身体だけでなく感情の起伏も薄くなってきたように感じられました．

夏の晴れたある日，むせ返るような暑さのなか，渋谷の人混みをかき分け友人とショッピングに出かけていました．逃げ込むように入ったスクランブルスクエアにはナイキが入っており，ふと目を挙げると，普段なら意識もしないような筋骨隆々としたマネキン達が目にとまりました．あぁ，綺麗にライトアップされたこのウェアも，私には似合わないのだろうな，と思ったその時，場を持たせようとサービス精神がふと口を衝いて出てきました．

「足の速い奴ってモテたよな」

その日は珍しく思いつきが形になりました．店員さんの言うがままシューズとウェアを購入し，気がつくと満足げにウイスキーを飲んでいました．振り返ると，何か無意識の抑圧が警鐘を鳴らしていたのかもしれません．

何はともあれ，私は翌日最初のランニングへと足を運びました．息を荒げ休憩を挟みながら走ったのはたったの3km．心拍数はあっという間に190になり，休憩を除いたペースは6.5分/kmでした．その日は筋肉痛で動けませんでした．三日坊主でも良いか，そう思いましたが，その翌日には走っていました．

〜中略〜

1ヶ月後，気がつくとハーフマラソンにエントリーしていました．

焦り

ノリでエントリーした瞬間，言語化できない焦りから，脳は快楽に包まれました．気を取り直し机に向かい整理したのが以下です．

心肺機能がもたない
- 3kmほどで息は上がり，心臓はドラムンベースより速いBPMを刻みます．無理です．
負傷するかもしれない
- 不健康体がいきなり走り始めたわけですので，おじいさんのような脚を怪我する可能性がありました．
そもそも走りきれない
- 当時，1回の走行距離は最長でも8kmほどでした．21kmは想像もできません．
足が遅い
- 出るからには遅すぎるのは嫌でした．

良い歳した大人のアプローチ

今年で27になりました．もう良い大人です．良い大人の良いところは，経験豊富なことです．焦りは認識と対策の不足，期待に対する不確実性からくることを知っていますので，まずは情報収集から始めました．厳密な定義は避けることにし，簡単に整理します．

【よく知られるトレーニング】

ジョギング：会話が続くぐらいゆっくり走る．気楽
ペース走：一定のペースで一定の距離を走る．息ははずむ
ロング走：20~30km などの長い距離を走る．ハーフマラソンには不要
インターバル走：一定ペースで一定距離，速く走るのと遅く走るのを繰り返す．キツすぎる．やりたくない
LSD (Long Slow Distance)：ジョギングよりも遅く，長時間走る．楽しいが足きつい
筋トレ：マッチョ

【3つの心拍数】

最大心拍数：最大限追い込んだときの心拍数．ノイズは入るがスマートウォッチで何回か確かめる．
安静時心拍数：座ってtwitterを眺めているときの心拍数
レンジ：最大心拍数 - 安静時心拍数．ここをどのぐらい攻めるかが運動の強度

【パフォーマンスと密接に関わるらしい数値】

VO2max：最大酸素摂取量．エネルギーを燃やせる限界に相当する
AT値：無酸素性閾値．ここを超えると無酸素運動になり続かない
LT値：乳酸性閾値．乳酸を再代謝できるペース．AT値とほぼ同じっぽい
ランニングエコノミー：出力と酸素消費の比率．いかに省エネで走れるか

取り組み

ここからは，ズブの素人がいかにして効率良く足を速く"した"かを共有しようと思います．あくまで素人です．いくら文献を引いているとはいえ間違っている可能性はあるのでご注意を．

立てたトレーニング戦略

webの記事やYoutubeを色々と漁りましたが，結局何をすべきかうまく pooling することはできませんでした．そこで，信頼すべきはやはりサイエンスだろうということで，9月ごろからスポーツ科学の論文を読んでみることにしました．その結果，最も意識すべきは，VO2max を伸ばすことだと判断しました．

VO2maxが有酸素運動のパフォーマンスに最も影響するということは，様々な研究で共通していました． Pate and Kriska (1984) は，有酸素運動のパフォーマンスを説明する3つの主要因を組み込んだモデルを開発しています．それは，VO2max，LT値，ランニングエコノミーです．このモデルは，Hoff et al. (2002) や Helgerud (1994) など後の多くの研究結果によって指示されています．また，このなかでも VO2max が最も重要な要素であることが指摘されています (Saltin, 1990)．さらに，上述のLT値も，VO2maxに応じて変化するとのことです (Mcmillan, 2005)．よって，VO2maxさえなんとかすれば息切れは解消し，より楽に走れるようになると考えました．

VO2maxを向上させるには，どのようなトレーニング戦略をとれば良いでしょうか．多くの研究では，インターバル走が適していると結論付けられています (Astorino et al., 2017; Milanović et al., 2015)．また，後で紹介する Helgerud et al. (2007) では，インターバル走以外の持久トレーニングは効果が無いとさえありました．

ランニングエコノミーについては，細胞内のエネルギー向上であるミトコンドリアの増加による代謝向上，筋肉の剛性・柔軟性向上による弾性エネルギーの効率化，フォームの効率化などが寄与するそうです (Hoff et al., 2002)．フォームに関しては文字で読んでもよく分からなかったため，Youtubeで勉強することにしました．

後で紹介する論文も鑑み，結論として，以下のようなトレーニング戦略を立てることにしました．

【戦略】

平日はインターバル走を，疲れているときはペース走かジョグ（5km程度）をする
- 朝は起きれないので夜やります．仕事中にウェアに着替えておくと，退勤ダッシュできます．
- 夜は倒れるように寝ます．
週末は時間が取れる（本当か？）ので，LSDまたは長めのジョグをする．
- 友人を誘いやすいのもよかった．
走った次の日は休む
練習前後に柔軟，ウィンドスプリントをする．
余裕のある日に下半身の筋トレをする．
膝が痛くなったら完治するまで休む．
お酒は我慢しない（超重要）

結果

まずは，apple watch が推定する VO2max の推移を載せてみます．トレーニングの甲斐もあり，レース直前までしっかり伸ばすことができました． 6月以前はまったく運動していないのでまともに測定できていませんね．笑

f:id:kur0cky:20211216014036j:plain

そしてハーフマラソンでは，目標としていた2時間を切ることができました．

その時の記録がこちらです．これは参加者の上位36%のペースでした．最初の3km走（笑）よりはるかに速いスピードです．

f:id:kur0cky:20211216014044j:plain

すっかり走るのが楽しくなってしまい続けているわけですが，それ以外にもメリットはたくさんありました．ただ，デメリットもあるのでいくつか整理しておきます．

メリット

メンタルに非常に良い
身体が絞られる
よく寝れる
疲れにくくなる
達成感がすごい

デメリット

疲れる
脚の色々な箇所が痛くなる
走らないとストレスが溜まるようになる
結構な時間が失われる

特に，メンタルへの効果は劇的なものがありました．

論文紹介（本題）

さて，ここからが本題です．正直，私の特に面白くもない振り返りはどうでも良いです．情報収集の過程で役に立ったと思う論文をかいつまんで紹介します．

1本目：Aerobic High-Intensity Intervals Improve VO2max More Than Moderate Training (Helgerud et al., 2007)

前述の通り，VO2max がマラソンのパフォーマンスに寄与すること，インターバル走はほぼ間違いなさそうでしたので，効率的に向上させるための練習を調べました．

【背景・課題】

VO2max向上にはインターバル走が良いという研究はたくさんある．
異なる強度のトレーニングを，エネルギー消費量を合わせた上での比較はされてこなかった．
- これは，仕事や私生活にできるだけ影響を及ぼしたくなかった私には大切な要素でした（効果がいくらあっても私生活に影響してはまずい）．

【方法】

被験者40人を4グループにランダムに分け，それぞれ異なるトレーニングを8週間行う．
- 心拍数140程度の LSD 45分
- 心拍数170程度の LTペース走 25分
- 心拍数185程度の 15秒インターバル走47回．間は15秒のゆっくりジョグ
- 心拍数185程度の 4分インターバル走4回．間は3分のゆっくりジョグ

【結果】

VO2max は 2つのインターバル走グループで有意に向上
一方，LSDとLT群では VO2max に変化はなかった（HRmaxが70~85%のトレーニング）．血液の拍出量が変化しない．
15秒の短いインターバルでは心拍数が上がりきらず，4×4min などのより長い時間のインターバルが推奨される．

f:id:kur0cky:20211219020447p:plain

2本目：National Athletic Trainers' Association Position Statement: Prevention of Anterior Cruciate Ligament Injury (Padua et al.,2018)

トレーニング戦略を組む上で，パフォーマンス向上の他に常に気にしなければならなかったのが，怪我への意識でした．特に，膝周りには主要な靭帯が複数あり，最も故障しやすいことがすぐにわかりました．予防のためのトレーニングを行うべく調査を進めたところ，国際アスレチックトレーナー協会が声明を出した論文として Padua et al. (2018) が見つかりましたので，これを参考にすることとしました．

【背景・課題】

下半身の負傷はスポーツ関連の全負傷の66％を占めており，膝が最も一般的に負傷している関節である．
- 特に重要で壊滅的な膝の損傷は，ACL（前十字膝靭帯）の損傷であり，生涯にわたって5000人あたり1〜5人のACL損傷が発生している．
ACL損傷の予防には多くの先行研究があり，多要素からなるトレーニングが重要だとされてきた．
- 多要素トレーニングにより，ACL損傷リスクは 39%~73% 減少する (Sugimoto et al., 2012)．
- 単一の最適な予防トレーニングプログラムを特定した研究はない．
- 中には検出力を欠いていたり，コンプライアンスが不十分である研究もある．これらを統合するメタアナリシスが重要である
- 故障する可能性がある負荷を被験者にかけるのは倫理に反する．RCTはできない
それぞれのトレーニングはどのようなバランスで組み合わせれば良いかは不明である．

【目的】

非接触型および間接型の ACL損傷の予防に関する最新のベストプラクティスの推奨事項を提供する．
多要素トレーニングプログラムを開発するための一般的なガイドラインを提供する．
効果的な予防トレーニングプログラムの大半は、筋力、プライオメトリクス、敏捷性、バランス、柔軟性のうち少なくとも3種類の運動について、適切な運動技術に関するフィードバックを含む多成分の運動プログラムを組み込んだものである。

【方法】

既存研究を網羅的にサーベイし，統合する
既存研究で用いられている予防トレーニングを体系的に分類し，傾向を明らかにする

【結果】

ACL損傷を予防する効果的な多要素トレーニングプログラムは，下表のように整理されるとのことでした．プログラムを構成する個々のトレーニングは，からなり，これらから複数を組み合わせ，フィードバックをすることが重要であるとわかります．

筋力
プライオメトリクス（筋肉の瞬発力）
敏捷性
バランス力
柔軟性

f:id:kur0cky:20211219030132p:plain — Table. Common Types of Exercises Included in Multicomponent Anterior Cruciate Ligament Injury-Prevention Training Program(Padua et al.,2018)

また，この分類のより詳細としては，下表のように具体的トレーニングな網羅的にリストアップされていました．

f:id:kur0cky:20211219030144p:plain — Table. Specific Strength, Plyometric, Agility, Balance, and Flexibility Exercises That Have Been Incorporated Into Multicomponent Anterior Cruciate Ligament Injury–Prevention Training Programs (Padua et al.,2018)

他の詳細な議論は省略しますが，結論として，以下の提言がなされていました．

筋力，プライオメトリクス，敏捷性，バランス力，柔軟性からすくなくとも3つ以上のトレーニングを選択肢，組み合わせる．
それぞれを15分以上かけ，本格的なトレーニングの前後に行う
これを週に2〜3回以上行う

おわりに

いかがでしたでしょうか．私は4月の長野マラソンにエントリーしました．当たることを願っています．貴殿はいかがなさいますか？

良いお年を．

参考文献

Astorino, T. A., Edmunds, R. M., Clark, A., King, L., Gallant, R. A., Namm, S., ... & Wood, K. M. (2017). High-intensity interval training increases cardiac output and VO2max. Med Sci Sports Exerc, 49(2), 265-273.
Helgerud, J. (1994). Maximal oxygen uptake, anaerobic threshold and running economy in women and men with similar performances level in marathons. European journal of applied physiology and occupational physiology, 68(2), 155-161.
Helgerud, J., Høydal, K., Wang, E., Karlsen, T., Berg, P., Bjerkaas, M., ... & Hoff, J. (2007). Aerobic high-intensity intervals improve V˙ O2max more than moderate training. Medicine & science in sports & exercise, 39(4), 665-671.
Hoff, J., Gran, A., & Helgerud, J. (2002). Maximal strength training improves aerobic endurance performance. Scandinavian journal of medicine & science in sports, 12(5), 288-295.
Mcmillan, K., Helgerud, J., Macdonald, R., & Hoff, J. (2005). Physiological adaptations to soccer specific endurance training in professional youth soccer players. British journal of sports medicine, 39(5), 273-277.
Milanović, Z., Sporiš, G., & Weston, M. (2015). Effectiveness of high-intensity interval training (HIT) and continuous endurance training for VO 2max improvements: a systematic review and meta-analysis of controlled trials. Sports medicine, 45(10), 1469-1481.
Padua, D. A., DiStefano, L. J., Hewett, T. E., Garrett, W. E., Marshall, S. W., Golden, G. M., ... & Sigward, S. M. (2018). National Athletic Trainers' Association position statement: prevention of anterior cruciate ligament injury. Journal of athletic training, 53(1), 5-19.
Pate, R. R., & Kriska, A. (1984). Physiological basis of the sex difference in cardiorespiratory endurance. Sports Medicine, 1(2), 87-89.
Saltin, B. (1990). Maximal oxygen uptake: limitations and malleability. International Perspectives in Exercise Physiology, K. Nazar and RL Terjung (Eds.). Champaign, IL: Human Kinetics Publishers, 26-40.
Sugimoto, D., Myer, G. D., McKeon, J. M., & Hewett, T. E. (2012). Evaluation of the effectiveness of neuromuscular training to reduce anterior cruciate ligament injury in female athletes: a critical review of relative risk reduction and numbers-needed-to-treat analyses. British journal of sports medicine, 46(14), 979-988.

2020-12-05

サウナーの皆さん，論文読んでますか？

こんにちは．表参道で働くサウナーことkur0ckyです．最近は，武蔵小山温泉清水湯によく行きます．

本記事は，Sansan Advent Calendar 2020 の5日目の記事です．

それではやっていきます．

長めの前書き
サウナ研究の紹介
- 1. サウナと健康の関連について
  - 血流や脈拍，血圧の上昇
  - 交感神経系への刺激
2. コロナウイルスによるサウナ習慣への影響
- 目的
- 方法
- 結果
- 感想
おわりに
参考文献

長めの前書き

突然ですが，サウナは好きですか？僕は大好きです．

サウナって気持ちいいですよね．寒いとき，暑いとき，仕事が大変なとき，嬉しいことがあったとき，報われない感情に身を焦がすとき．．．体調さえ良ければ，サウナはどんな状況でも人生を華やかに彩り，「ととのい」の世界へと私たちを誘ってくれます．

ところで，皆さんはサウナに入っているとき何を考えますか？テレビを見ていますか？時計を眺めていますか？それとも，滴る汗に思いを馳せ，瞑想しているでしょうか．人生について考えるのも良いですね．

ここまででお気づきの方も多いでしょうが，サウナを楽しむ術が多ければ多いほど，一部の隙もなくサウナを堪能することができるようになります．そこでこの記事では一つ，サウナをより楽しむ方法をお伝えしたいと思います．

それは，「サウナに関連する論文を読む」ことです．

あまり知られていないことですが，サウナについても様々な研究が存在し，たくさんの学術論文が出版されています．ためしに，Google Scholar で "sauna bathing" と検索してみてください．蓄積されてきた研究の数に驚くことでしょう．これらの論文を読み，サウナについてより深くを知ることで，サウナをより楽しめるようになります．サウナにはどのような効果があるのか，なぜ気持ちいいのか，サウナ文化はどのように醸成されてきたのか，色々な角度からサウナを知ることができます．これはいうなれば，「サウナ鑑賞」です．音楽や絵画で考えると分かりやすいと思います．背景について知り，様々なものを何度も体験し，素養を身につけることが味わいや楽しみに幅を持たせるのです．

ここで一つ注意ですが，たとえサウナの負の側面に関する議論を見つけても，決して気を落とさないでください．そうです．サウナが好きな人は，健康に良かろうが悪かろうがサウナに入ってしまうでしょう．どうせなら不安を感じながらサウナに入るよりも，楽しみながら入るほうが気持ちいいに決まってます．あくまでもサウナを楽しむことが目的ということを忘れないでください．

それでは，みなさまのサウナ生活がより豊かになる助けとなるため，サウナに関連する様々な研究を紹介していきます．

サウナ研究の紹介

1. サウナと健康の関連について

サウナの研究トピックとして最も目にするのは，やはり健康との関連です．サウナが気持ちの良いことは間違いないですが，健康への善し悪しは誰もが知りたいところなのでしょう．最近では，Laukkanen et al. (2018) や Hussain et al. (2019) などのサーベイ論文も出てきており，より網羅的に知りたい方はこれらを読むことをおすすめします．

さて，これらのサーベイを見ると，サウナが健康に及ぼす影響のほとんどが，「身体を温めることによる血流や脈拍の増加」，もしくは「高温による交感神経系への刺激」に由来しているようです．そこでこの章では，特にこの2点に絞り，より簡潔（しかし雑）な紹介をしていきます．

血流や脈拍，血圧の上昇

S.Ketelhut and R.G.Ketelhut (2019) は，サウナ中とサウナ後の血圧と心拍数の変化を調査しています（ただしサンプルサイズは19と少ない）．フィンランドで一般的な約80℃のサウナでは，心拍数は分間120 ~ 150まで上昇するとともに，有意に血圧が上昇するようです (p < 0.01)．中程度の運動に相当するような負荷です．一方で，サウナ後は血圧は急速に低下し，入浴後30分でも，入浴前と比べて有意に低くなるようです(p < 0.01)．別の研究では，短期的な血圧低下だけでなく，サウナが長期的な血圧の低下さえ促し，心血管の機能を向上させることを示唆しています (Lee et al., 2020)．

継続的なサウナ習慣による長期的な血圧への影響を調査したものはどうしても限られてしまいますが，私の知る範囲で2つ紹介します．

Zaccardi et al. (2015) は1621人の男性を24.7年間にわたり追跡し，頻繁に入浴（週4~7回）する男性は，高血圧発症リスクが47%も減少することを示しています．標本は一般募集で無作為標本ではなく一般募集ですが，アルコール摂取量や経済力，心肺機能 (CRF) などいくつかの交絡因子を調整していました．どうやら，定期的なサウナ入浴は全身血圧の低下に効く可能性がありそうです．

Laukkanen et al. (2020)は，20.7年間にわたり2315人のフィンランド人を追跡し，サウナの入浴頻度・入浴時間と，心突然死・冠動脈性心疾患による死亡・心血管疾患による死亡との関連を調べています．結果として，上記のすべてのリスクが，サウナの入浴頻度が高いほど低下することを示しています．

なんだか，とにかく心臓の血管には良さそうですね．週4回以上の入浴はハードですが．．．

交感神経系への刺激

サウナは多数のホルモンに作用するようです．たとえば，コルチゾールや血漿レニン，ノルエピネフリンの分泌が増加することが知られています (Laukkanen et al., 2018). コルチゾールはタンパク質の代謝や脂肪の分解の促進，炎症を抑える働きがあり，ステロイド系の炎症薬にも使われます．また，ノルエピネフリンは交感神経を活性化する代表的な神経伝達物質で，特にストレスを感じた時や運動時に放出されます．筆舌に尽くしがたい「ととのい」の快楽とも関係があるのでしょうか（謎）．

最近のサーベイとしては，サウナとホルモンの関係は Huhtaniemi and Laukkanen (2020) によくまとまっています．これによると，サウナに慣れている人はノルエピネフリンをより多く分泌する傾向にあること，発汗により利尿を阻害するホルモンが増加することなどが参考文献とともに示されています．ただし，これらのホルモン反応は短いものであって，入浴後はすぐに正常に戻るそうです．

私としても気になる懸念としては，高温による精子への悪影響があります．しかしHuhtaniemi and Laukkanen (2020)は，特にサウナ経験のない男性では精子の生産が減少するが，サウナ習慣と生殖能力の低下は関連しないことにも言及しています．これは嬉しいですね．

特に運動後のサウナに着目した研究に Rissanen et al. (2020) があります．サウナ自体が負荷の高い運動のようなもので，次のトレーニング前24時間の入浴は推奨されないとまとめています．十分余裕のある時に入浴したいですね．

2. コロナウイルスによるサウナ習慣への影響

驚くべきことに，サウナとコロナウイルスをテーマにした論文が既に出版されています．その中から1つ，"Sauna bathing frequency in Finland and the impact of COVID-19" (Likkanen and Laukkanen, 2020) という論文を紹介します

この論文では，COVID-19（コロナウイルス）の流行によって，フィンランド人のサウナ入浴頻度がどの程度影響を受けたかを調査しています．

目的

フィンランドは，世界でもっともサウナ文化の進んだ国です．しかしCOVID-19の流行により，フィンランドの公衆サウナも大規模な閉鎖を余儀なくされてしまいました．そこでこの論文では，あまり知られてこなかったフィンランド人のサウナ入浴頻度と，コロナ禍におけるその変化を調査することを目的としています．

方法

2020年5月，市場調査会社 Bilendii によって抽出された1000人のフィンランド人を対象に，アンケート調査を実施しています．標本は性別，場所，年齢，収入，職業，住居の種類などを鑑み，フィンランド人の良い代表となるように調整がとられているそうです．調査項目は，入浴頻度，考えられる変化，その理由，感染への懸念などです．

結果

コロナ禍以前では，なんと60％のフィンランド人が週に1度はサウナに入っていました．中央値は週に2~3回です．さすがサウナ大国フィンランドですね．

サウナの入浴頻度に大きく関わるのは，住居の種類です． 89％の人が個人所有のサウナを利用していたが，block building（マンションやアパート？）では 64％に留まるそう．一方で戸建住宅に住んでいる人は，性別に関係なく，週4回以上入浴する人が block building に住んでいる人よりも約3倍多い結果となっています（12.6％と4.4％）．

この住宅による傾向は，コロナ禍でも顕著になっています．その結果を下表に引用しました．

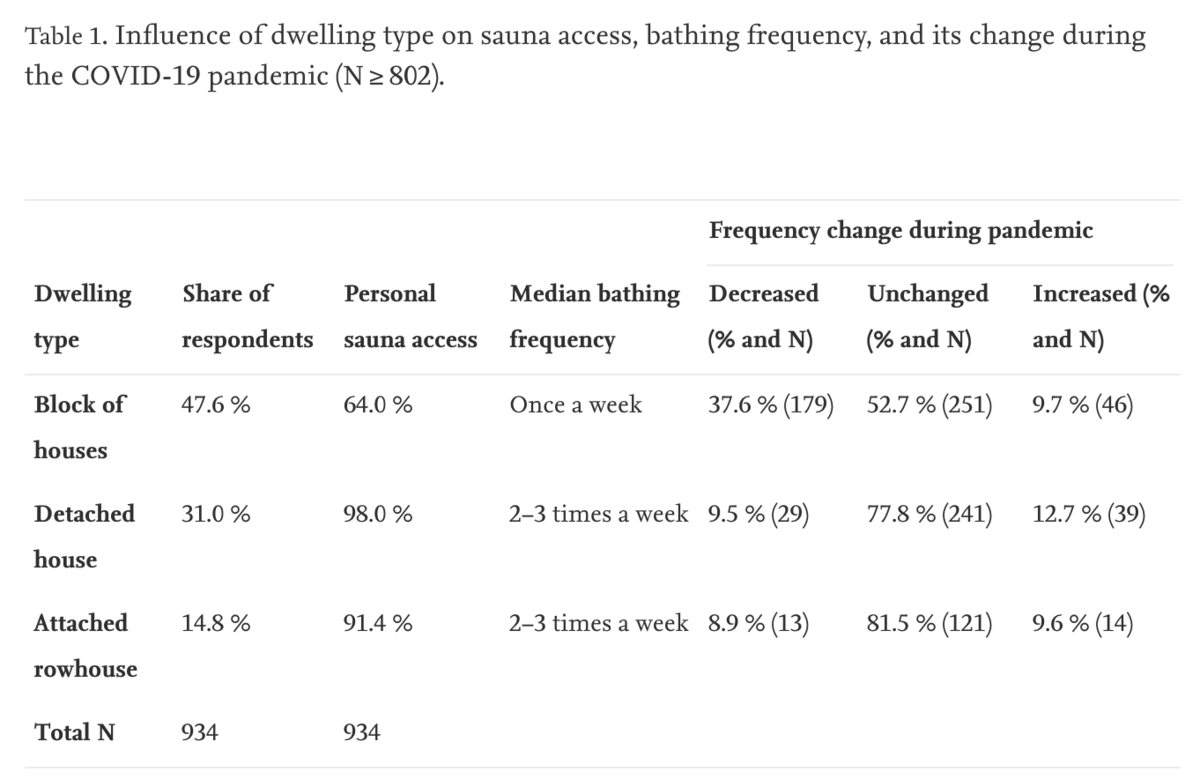
f:id:kur0cky:20201204165430p:plain

コロナ禍に入ると，回答者の23％は入浴頻度を減らしていますが，そのうちの81%は block building の居住者です．一方で，より頻繁に入浴するするようになった11％の回答者のうち，戸建てや長屋に住んでいる人は59%です．

また，公衆サウナの閉鎖に関しては，74%が同意しているそうです．感染リスクは一定感じながらも，大半の人は家にサウナがあるので我関せずということでしょうか．

感想

恐るべし，フィンランド．

まさにサウナ天国ですね．なんと89%のフィンランド人が personal なサウナにアクセスできるそうです．羨ましい限り．．．これだけ環境が整っているのであれば，サウナ文化が衰退することはなさそうですね．元々どのような公衆サウナがあったのかは興味深いところですが，かえって日本の方が充実していたのかもしれません．

おわりに

サウナーがサウナ論文を読む意義と，いくつかのサウナ研究を紹介しました．サウナに入りながら，自分の身体に何が起きているのかを想像すると，ワクワクしてきますね．本場フィンランドでは一般的な personal サウナに恋い焦がれるのも良いですね．クリスマスはイルミネーションの綺麗なサウナでも探して行ってみようかと思います．

それでは，みなさんのサウナ人生が少しでも豊かにならんことを．

参考文献

Huhtaniemi, I. T., & Laukkanen, J. A. (2020). Endocrine effects of sauna bath. Current Opinion in Endocrine and Metabolic Research, 11, 15-20.
Hussain, J. N., Greaves, R. F., & Cohen, M. M. (2019). A hot topic for health: Results of the Global Sauna Survey. Complementary therapies in medicine, 44, 223-234.
Ketelhut, S., & Ketelhut, R. G. (2019). The blood pressure and heart rate during sauna bath correspond to cardiac responses during submaximal dynamic exercise. Complementary therapies in medicine, 44, 218-222.
Laukkanen, T., Khan, H., Zaccardi, F., & Laukkanen, J. A. (2015). Association between sauna bathing and fatal cardiovascular and all-cause mortality events. JAMA internal medicine, 175(4), 542-548.
Laukkanen, J. A., Laukkanen, T., & Kunutsor, S. K. (2018, August). Cardiovascular and other health benefits of sauna bathing: a review of the evidence. In Mayo clinic proceedings (Vol. 93, No. 8, pp. 1111-1121). Elsevier.
Lee, E., Willeit, P., Laukkanen, T., Kunutsor, S. K., Zaccardi, F., Khan, H., & Laukkanen, J. A. (2020). Acute effects of exercise and sauna as a single intervention on arterial compliance. European journal of preventive cardiology, 27(10), 1104-1107.
Liikkanen, L. A., & Laukkanen, J. A. (2020). Sauna bathing frequency in Finland and the impact of COVID-19. Complementary Therapies in Medicine, 56, 102594.
Rissanen, J. A., Häkkinen, A., Laukkanen, J., Kraemer, W. J., & Häkkinen, K. (2020). Acute Neuromuscular and Hormonal Responses to Different Exercise Loadings Followed by a Sauna. The Journal of Strength & Conditioning Research, 34(2), 313-322.
Zaccardi, F., Laukkanen, T., Willeit, P., Kunutsor, S. K., Kauhanen, J., & Laukkanen, J. A. (2017). Sauna bathing and incident hypertension: a prospective cohort study. American journal of hypertension, 30(11), 1120-1125.

2020-09-21

「大規模計算時代の統計推論」を全部Rでやってみる ~第4章~

R CASI 大規模計算時代の統計推論

こんにちは，kur0ckyです．夏もやっと終わりが見え，涼しい日には好きな長袖が着れて嬉しいです．秋はめっちゃ好きです．

さて，今回扱う第4章は「フィッシャー派的な推論と最尤推定」です． 3章までは，頻度派とベイズ派の二軸で説明されてきましたが，ここで新たに「フィッシャー派」というもう一つの流派が出てきました．また，4章のはじめには次のような記述があります．

「分散分析」「有意差検定」「最尤推定」は，ほとんどいつも頻度派的に適用されてきた．しかし，それらフィッシャー派の手法の理論的根拠の多くは，実際にはベイズ派と頻度派のいずれの発想にもよらないものであり，時には両者の組み合わせによるものであった．

しっかり読んでいくことで，「フィッシャー派」がどのような立ち位置にあるのか，理解したいです．できないかもしれません．それではやっていきましょう．

4.1 尤度と最大尤度
- 基本的な概念
- 図4.1（正規分布とガンマ分布の最尤推定）
4.2 フィッシャー情報量と最尤推定
4.3 条件付き推論
4.4 並び替えと無作為化
- 図4.3
- 疑問点
おわりに

4.1 尤度と最大尤度

まずは最尤推定のおさらいです．基本的な概念をさらった後，腎臓病患者のgfrデータを元にいくつかの分布のパラメータを最尤推定する例が紹介されています．

基本的な概念

なんらかの確率モデルを仮定したとき，そのモデルのもと観測値 $\bf x$ が得られる確率を尤度 (likelihood)といいます．また，観測値を定数とし，パラメータ $\mu$ の関数と捉えたものを尤度関数 (likelihood function)といったりします．つまり，尤度関数 $L _ {\bf x}(\mu)$ は次で表されます．

$L _ {\bf x}(\mu) = p({\bf x} | \mu).$

さらに， $\bf x$ の各要素が独立に観測されるとしたとき，尤度関数は単純な積の形に分解できます．

$L _ {\bf x}(\mu) = p({\bf x} | \mu) = \prod _ {i} p(x _ i | \mu).$

この尤度関数の自然対数をとったものを，対数尤度関数(log likelihood function)といい，ここでは $l _ {\bf x} = \log L _ {\bf x}(\mu)$ と表します．対数をとることにより，和の形で表すことができます．積の形のままでは， $L _ {\bf x}(\mu)$ があっという間に小さくなってしまうことがありますが，和の形ではこれを防ぐことができます．もちろん，単純に扱いやすいこともメリットです．そして，この対数尤度を最大にするようなパラメータの値が最尤推定値 (maximum likelihood estimate; MLE)です．モデルのパラメータの関数になっているような量に興味がある場合は，もちろん最尤推定値を差し込んでも良いです．

$\text{MLE : }\hat\mu = \text{argmax} _ {\mu \in \Omega} l _ {\bf x}(\mu).$

ちなみに，前回の記事でも紹介しましたが，最尤推定値は無情報事前分布を用いた場合のMAP推定値（事後分布を最大にするような推定値）と同じになります．無情報事前分布は一様（定数）であるためです．

$\mu _ {MAP} = \text{argmax} _ {\mu} p(\mu|{\bf x}) = \text{argmax} _ {\mu}p({\bf x}|\mu)p(\mu) = \text{argmax} _ {\mu}p({\bf x} | \mu)$

そのため，本書でも

最尤推定は妥当なベイズ派の正統性も有している．

という記述があります．

図4.1（正規分布とガンマ分布の最尤推定）

さっそく解析例です． 2章でも扱った腎臓病患者のgfrデータをもとに，正規分布とガンマ分布の母数を推定してみましょう．通常ガンマ分布の下限は $x \geq 0$ なのですが，本書では様々な下限 $\lambda$ をとりうるようにした分布に対して推定を行っています．この特殊なガンマ分布は次式で表されます．

$\displaystyle f _ {\mu} (x) = \begin{cases} \frac{(x - \lambda) ^ {(x - \nu)}}{\lambda ^ {\nu}\Gamma(\nu)}\exp(-\frac{x-\lambda}{\sigma}) & x > \lambda, \\\ 0 & x \leq \lambda. \end{cases}$

正規分布やガンマ分布の場合は，最尤推定値が解析的に求まるのですが，この特殊な場合は求まらないそうです．この記事では，面倒なので全部数値的に求めてしまいます．笑

それではやっていきましょう．まずはパッケージを読み込み，データをダウンロードします．

library(tidyverse)
library(stats4)

theme_set(theme_classic(base_family = "HiraKakuPro-W3"))

gfr <- scan("https://web.stanford.edu/~hastie/CASI_files/DATA/gfr.txt")

Rには最尤推定をするための様々なパッケージがありますが，ここではstats4パッケージのmle()を使ってみることにします． stats4は追加のインストールが必要なく，歴史も長いです．アルゴリズムはシンプルに準ニュートン法を使うことにします．

mle()には，負の対数尤度関数を引数に要求し，これを最小化します（つまり対数尤度の最大化です）．対数尤度関数を用意しましょう．せっかくなので普通のガンマ分布も推定します．正規分布と普通のガンマ分布はそれぞれdnorm(), dgamma()が密度関数として用意してあるので非常に簡単です．下限が0でないガンマ分布の対数尤度は，少し計算して次のようになります（ただし $x > \lambda$ で）．

$\displaystyle l _ {\bf x}(\lambda, \sigma, \mu) = \sum _ i \left ( (\nu -1)\log (x _ i - \lambda) - \nu \log(\sigma) - \log(\Gamma(\nu)) - (x _ i -\lambda) / \sigma \right) .$

# 正規分布
neg_LL_normal <- function(mu,sigma) {
  x = gfr
  -sum(dnorm(x, mean=mu, sd=sigma, log = T)) 
}

# 普通のガンマ分布
neg_LL_gamma <- function(shape, rate){
  x = gfr
  -sum(dgamma(x, shape, rate,  log = T))
}

# 下限が自由なガンマ分布
neg_LL_gamma2 <- function(lambda, sigma, nu){
  x  = gfr
  ll = (nu - 1) * log(x - lambda) - nu * log(sigma) - log(gamma(nu)) - (x - lambda) / sigma
  ll[x < lambda] = 0
  -sum(ll)
}

準備ができたので最適化していきましょう．数値的な発散によるエラーを避けるため，少しズルをして初期値をうまく与えています．本当なら，様々な初期値を用意して，最も対数尤度が大きくなる値を選ぶべきでしょう．

normal_fit <- mle(minuslogl = neg_LL_normal,
                  start=list(mu=50, sigma=10),
                  method = "L-BFGS-B",
                  upper = c(Inf, Inf),
                  lower = c(-Inf, 0))
gamma_fit <- mle(minuslogl = neg_LL_gamma,
                 start=list(shape = 50, rate = 0.1),
                 method = "L-BFGS-B")
gamma2_fit <- mle(minuslogl = neg_LL_gamma2,
                 start=list(lambda = 21.5, sigma = 5.5, nu = 6),
                 method = "L-BFGS-B")

最後に図を書いて終わらせます．推定値はfit@coefに入っています．

colors <- c(normal = "black",
            gamma = "blue",
            truncated_gamma = "steelblue")
tibble(gfr = gfr) %>% 
  ggplot()+
  geom_histogram(aes(gfr, y = ..density..), 
                 colour = "black", fill = "green", size = .3)+
  stat_function(fun = dgamma2, aes(colour = "truncated_gamma"),
                size = 1, linetype = 2,
                args = list(lambda = gamma2_fit@coef["lambda"],
                            sigma = gamma2_fit@coef["sigma"],
                            nu = gamma2_fit@coef["nu"]))+
  stat_function(fun = dgamma, aes(colour = "gamma"),
                size = 0.5,
                args = list(shape = gamma_fit@coef["shape"],
                            rate = gamma_fit@coef["rate"]))+
  stat_function(fun = dnorm, aes(colour = "normal"), size = 1,
                args = list(mean = normal_fit@coef["mu"],
                            sd = normal_fit@coef["sigma"]))+
  scale_colour_manual(values = colors)+
  scale_x_continuous(limits = c(15, 118))+
  labs(x = "gfr", y = "頻度")

綺麗な図がかけました．今回は関数のプロットにstat_function()を使いました． stat_function()は，引数argsにリストを渡す形でパラメータを指定することができます．ちなみに，この中では尤度，AICともに下限が自由なガンマ分布が良くなるようです．

f:id:kur0cky:20200921162504p:plain

4.2 フィッシャー情報量と最尤推定

フィッシャー派の大本命であろうと思われるフィッシャー情報量について書かれた節です．解析がないのですっ飛ばします．

フィッシャー情報量については前回の記事でもチラッとだけ紹介しました（ほぼ他の記事に丸投げでしたが）．

kur0cky.hatenablog.com

4.3 条件付き推論

この節では条件付き推論 (conditional inference) と補助統計量 (ancillary statistic) について書かれています．補助統計量とは，着目するパラメータ $\mu$ と無関係な分布をもつ確率変数や統計量のことです．たとえば，この節の冒頭で出てくるコイン投げの確率変数などです． $\mu$ に関する推論を行う際，このような確率変数はある値に固定してしまってよいことになります．

この記事で扱うには少し重すぎるので，詳しくはwikipediaなどをご覧ください．余裕があれば，十分統計量やBasuの理論などと一緒に解説する記事を書きたいと思います．笑

en.wikipedia.org

図4.2（コーシー分布のフィッシャー情報量の例）

補助統計量の例のうち，コーシー分布の例は解析があるので，この記事でも再現します．この例を通して，観測されたデータから求めたフィッシャー情報量が近似的な補助統計量として振舞うことが感覚的に示されています．つまり，コーシー分布のフィッシャー情報量を計算しましょう．

解析の手順は大きく次の5ステップです

コーシー分布から大きさ20の標本を10000個発生させる．
それぞれの標本に対し，locationの最尤推定量 $\hat \theta$ を求める．
また，それぞれの標本に対し，観測情報量下限 $1/I({\bf x})$ を計算する．
$1/I({\bf x})$ の10分位点ごとに $\hat\theta$ の経験分散を求める．
分位点ごとの経験分散と，分位点ごとの中央値をプロットする．

ここで， $I({\bf x})$ は最尤推定量を差し込んだフィッシャー情報量を使った $n\mathcal I _ {\hat\theta}$ ではなく，最尤推定値を代入したもので，次式で表されます．

$\displaystyle I({\bf x}) = - \ddot l _ {\bf x} (\hat \theta) = - \frac{\partial ^ 2}{\partial\theta ^ 2} l _ {\bf x} (\theta) | _ {\hat\theta}.$

まずは，標本から「観測されたフィッシャー情報量」を計算する関数を作ります．まずは対数尤度の二回微分をしなければなりません．ゴリゴリ数式で攻めても良いのですが，全てRで解析する企画なので，微分もRでやってしまいます（楽してるわけではありません笑）． Rでは，expression()で対数尤度関数の数式オブジェクトを作っておき，D()で微分することができます．

f <- expression(log(1/pi/(1 + (x-theta)^2)))

D(D(f, "theta"), "theta")

綺麗に整理するところまではやってくれませんが，微分された数式が出てきます．これをコピペし，dd_ll_cauchy()という関数を作っておきましょう．

dd_ll_cauchy <- function(x, theta){
  -((1/pi * 2/(1 + (x - theta)^2)^2 - 1/pi * (2 * (x - theta)) * (2 * (2 * (x - theta) * (1 + (x - theta)^2)))/((1 + (x - theta)^2)^2)^2)/(1/pi/(1 + (x - theta)^2)) + 1/pi * (2 * (x - theta))/(1 + (x - theta)^2)^2 * (1/pi * (2 * (x - theta))/(1 + (x - theta)^2)^2)/(1/pi/(1 + (x - theta)^2))^2)
}

続いて標本を発生させ，location $\theta$ の最尤推定，そして「観測されたフィッシャー情報量」の算出まで一気にやってしまいます．

set.seed(1)
df <- tibble(index = 1:10000) %>% 
  mutate(x = map(index, ~  rcauchy(20, 0, 1))) %>% 
  mutate(theta_hat = map_dbl(x, ~ 
                               mle(minuslogl = function(theta){-sum(dcauchy(.x, location = theta, scale = 1, log = T))},
                                   start=list(theta = 0),
                                   method = "L-BFGS-B") %>% 
                               .@coef)) %>% 
  mutate(f_info = map2_dbl(x, theta_hat, ~ 
                           -1/sum(dd_ll_cauchy(.x, .y))))
print(df)

# A tibble: 10,000 x 4
   index x          theta_hat f_info
   <int> <list>         <dbl>  <dbl>
 1     1 <dbl [20]>   -0.132  0.113 
 2     2 <dbl [20]>    0.120  0.128 
 3     3 <dbl [20]>   -0.512  0.126 
 4     4 <dbl [20]>    0.0721 0.140 
 5     5 <dbl [20]>   -0.0773 0.183 
 6     6 <dbl [20]>    0.111  0.0983
 7     7 <dbl [20]>   -0.0705 0.108 
 8     8 <dbl [20]>    0.413  0.108 
 9     9 <dbl [20]>   -0.384  0.0799
10    10 <dbl [20]>   -0.118  0.0960
# … with 9,990 more rows

求めたフィッシャー情報量を100分率の区間 $(0-5), (5-15), \dots, (95-100)$ の分位点にわけ， $\hat\theta$ の経験分散を求めましょう． percent_rank()を使うとパーセンタイルが求まるので，それを100倍したものが区切りbreaksを上回っている数でグルーピングします．

# 10分位点の区切り
breaks <- c(seq(5, 95, 10), Inf)

df <- df %>% 
  mutate(percentile = percent_rank(f_info) * 100,
         rank = map_int(percentile, ~ sum(.x > breaks))) %>% 
  group_by(rank) %>% 
  summarise(f_info = mean(f_info),
            se = var(theta_hat)) %>%
  drop_na() 
print(df)

# A tibble: 11 x 3
    rank f_info     se
   <int>  <dbl>  <dbl>
 1     0 0.0547 0.0614
 2     1 0.0648 0.0682
 3     2 0.0728 0.0782
 4     3 0.0794 0.0830
 5     4 0.0863 0.0969
 6     5 0.0937 0.0997
 7     6 0.102  0.107 
 8     7 0.113  0.111 
 9     8 0.128  0.134 
10     9 0.157  0.186 
11    10 0.273  0.242

最後に作図です．今回は単純な散布図なのでコードも少なく，楽でした．

df %>% 
  ggplot(aes(f_info, se))+
  geom_point()+
  geom_abline(slope = 1, linetype = 2)+
  geom_hline(yintercept = 0.1, linetype = 2, colour = "red")+
  labs(x = "観測された情報量下限", y = "最尤推定量の分散")

f:id:kur0cky:20200915213030p:plain

疑問点

最尤推定量は一致推定量ではありますが，不偏推定量ではないですよね？？クラメル=ラオの下限は不偏推定量の中での話なので，この例のような比較を行うことには意味があるのか疑問に思いました．大きさ20のような小標本でも，今回の例のように，下限に近い値はでますよ，ということが言いたかったのでしょうか．大標本なら漸近的に不偏になるので良さそうですが．

おまけ：数式でやる

どうせなので，コーシー分布のlocationのフィッシャー情報量を数式でみましょう．コーシー分布の尤度関数は次式で与えられます．

$\displaystyle f({\bf x}| \theta) = \prod\frac{1}{\pi(1 + (x _ {i} - \theta) ^ 2)}.$

対数尤度を $\theta$ で微分したスコア関数は，素直に計算し次のようになります．

$\displaystyle \frac{\partial}{\partial \theta} \log f({\bf x}| \theta) = \sum \frac{\frac{2}{\pi(1 + (x _ {i} - \theta) ^ 2) ^ 2}(x-\theta)}{f(x _ {i}| \theta)} = \sum \frac{2(x _ i - \theta)}{1 + (x _ i - \theta)^ 2}.$

次に，スコア関数の二次モーメントは次のように計算できます．途中で $u = x-\theta, v = 1/(1 + u ^ 2)$ の置換積分をしています．最後はベータ関数の形を利用して整理しています．

$\displaystyle \begin{align} \mathcal I _ {x _ i} (\theta) &= {\rm E}\left(\left(\frac{\partial}{\partial \theta} \log f(x _ i| \theta)\right) ^ 2\right) \\\ &= \int _ {-\infty} ^ {\infty} \left(\frac{2(x _ i - \theta)}{1 + (x _ i - \theta)^ 2}\right) ^ 2 \frac{1}{\pi(1 + (x-\theta)^ 2)}dx \\\ &= \frac{4}{\pi} \int _ {-\infty} ^ {\infty} \frac{(x-\theta) ^ 2}{(1 + (x-\theta) ^ 2) ^ 3}dx \\\ &= \frac{8}{\pi}\int _ {0} ^ {\infty}\frac{u ^ 2}{(1 + u ^ 2) ^ 3}du \\\ &= \frac{4}{\pi}\int _ 0 ^ 1\sqrt{v}\sqrt{1-v} dv \\\ &= \frac{4}{\pi}\int _ 0 ^ 1 v ^ {3/2 - 1} (1-v) ^ {3/2 - 1} dv \\\ &= \frac{4\Gamma(3/2)\Gamma(3/2)}{\pi\Gamma(3/2 + 3/2)} \\\ &= \frac{4(0.5\sqrt{\pi}) ^ 2}{\pi 2!} = \frac{1}{2}. \end{align}$

よって，フィッシャー情報量はこの合計であり，

$\displaystyle \mathcal I _ {\bf x} (\theta) = \frac{n}{2}.$

となります．ありがとうございました．前節での例では，大きさ20の標本を作っているので，クラメルラオの下限は0.1となります．

4.4 並び替えと無作為化

$t$ 検定をはじめとする多くの手法は，標本が正規分布に従うことを仮定します．この仮定はしばしば現実てきでなく，批判にさらされます．本書では，これに対するフィッシャーの解決策として，並べ替えを利用したノンパラメトリック検定が紹介されています．

図4.3

まずはデータセットをダウンロードします．ついでに，対象の遺伝子である136行目を抜き出します．

leukemia <- read_csv("http://web.stanford.edu/~hastie/CASI_files/DATA/leukemia_big.csv")

leukemia_136 <- leukemia[136, ] %>% 
  unlist() %>% 
  unname()

シャッフルしないもとの $t$ 検定は1章でやっていたので，ここでは省略します．

続いて，データをシャッフルし47個の値と25個の値に分け，これに対して $t$ 検定します．これを $B = 10000$ 回やります． map()とnest()が大好きなので次のように実装しました．

B <- 10000
set.seed(1)

df_sim <- tibble(index = 1:B) %>% 
  mutate(split_index = map(index,~ sample(1:72, 25, replace = FALSE)),
         x1 = map(split_index, ~ leukemia_136[.x]),
         x2 = map(split_index, ~ leukemia_136[-.x]),
         t = map2_dbl(x1, x2, ~ t.test(.x, .y)$statistic))

print(df_sim)

次のようなtibble()ができます．何度でも推したいですがnest()は神です．

# A tibble: 10,000 x 5
   index split_index x1         x2              t
   <int> <list>      <list>     <list>      <dbl>
 1     1 <int [25]>  <dbl [25]> <dbl [47]> -1.66 
 2     2 <int [25]>  <dbl [25]> <dbl [47]>  0.662
 3     3 <int [25]>  <dbl [25]> <dbl [47]>  3.07 
 4     4 <int [25]>  <dbl [25]> <dbl [47]>  0.276
 5     5 <int [25]>  <dbl [25]> <dbl [47]> -0.950
 6     6 <int [25]>  <dbl [25]> <dbl [47]> -0.411
 7     7 <int [25]>  <dbl [25]> <dbl [47]>  0.752
 8     8 <int [25]>  <dbl [25]> <dbl [47]>  0.381
 9     9 <int [25]>  <dbl [25]> <dbl [47]> -0.853
10    10 <int [25]>  <dbl [25]> <dbl [47]>  0.895
# … with 9,990 more rows

ALLとAMLの間に差がないとする帰無仮説に対して有意水準を求めます． sum(abs(df_sim$t) >= 3.01) / Bで求めると0.0045となり，本書の0.0025とは少し離れてしまいましたが，乱数のせいにしておきましょう．

続いて作図します． annotate()で注釈や矢印を，geom_segment()でx軸のポイントをちまちまと書いていきます．軸ラベルのカスタマイズは，scale_x_continuous()内のbreaksで指定します．

df_sim %>% 
  ggplot(aes(t))+
  geom_histogram(fill = "gray100", colour = "steelblue",
                 bins = 50)+
  geom_vline(xintercept = -3.01, linetype = 2, colour = "red")+
  geom_vline(xintercept = 3.01, linetype = 2, colour = "red")+
  annotate("text", x = 3.5, y = 100, label = "もとのt統計量", family = "HiraKakuPro-W3")+
  annotate("segment", x = 3.5, xend = 3.1, y = 70, yend = 20,
           size=0.5, arrow=arrow(length=unit(0.30,"cm")))+
  scale_x_continuous(breaks=c(-4, -3.01, -2, 0, 2, 3.01, 4))+
  geom_segment(data = filter(sim, abs(t) > 3.01),
               aes(x = t, xend = t, y = 0, yend = -20),
               colour = "red", size = 0.3)+
  labs(x = "t*値",
       y = "頻度")

f:id:kur0cky:20200915213034p:plain

このようなシミュレーションによる検定は，正規分布の仮定をしなくても， $X _ i \sim f _ \mu (x)$ の独立同分布を帰無仮説として行うことができます．いわゆるノンパラメトリック検定の一つですね．ちなみに，この実験からは，ALLの遺伝子136の値に比べAMLの値が大きいと言えるかを判断することができますが，因果までは言うことができません．これと対照的な，有名なフィッシャーの農場実験の話題にも本書では触れられています．

疑問点

ただ，一つだけ疑問を感じたので，書いておきます．たしかに，帰無仮説 $X _ i \sim f _ \mu (x)$ のもとでは，シャッフルして分割した $72!/(42!25!)$ 通りの組み合わせは同様に確からしいです．しかし， $f _ \mu (x)$ を経験分布で近似すると考えると，並び替えではなく無作為に復元抽出するべきではないでしょうか．どちらが良いか私の弱い知識では判断できなかったので，どなたか教えてください（懇願）．．．

おわりに

内容もだんだんと骨太になってきました．少ししんどいですが細々とやっていきます．ではでは

2020-09-09

「大規模計算時代の統計推論」を全部Rでやってみる ~第3章~

R CASI 大規模計算時代の統計推論

こんにちは，kur0ckyです．

最近の出社と在宅の比率は半々ぐらいです．緊急事態宣言がでていた最後の方はメンタルきつかったのですが，今は落ち着いています．あまりの無気力さに，スーパーに行っても何も買う気が起きなかったりしていました．笑

第3章は，「ベイズ派的な推論」です．前章は頻度派のイントロでしたが，今回はそのベイズ版です．今回も前回に引き続き解析は少ないですが，それ以外にも初学では辛そうな知識や抽象的な記述が多いところは備忘録的に整理しています．誤りが多分にあると思うので，見つけたときは石を投げてください．現在読むだけなら半分ぐらいきてるのですが，この本はすごく勉強になってるので，買うと良いと思います．

大規模計算時代の統計推論: 原理と発展

作者:エフロン,ブラッドレイ,ヘイスティ,トレバー
発売日: 2020/07/30
メディア: 単行本

前回記事はこちらです．

kur0cky.hatenablog.com

それではやっていきます．

はじめに
3.1 2つの例
3.2 無情報事前分布
- ジェフリーズの事前分布
3.3 頻度派的な推論の欠陥
3.4 ベイズ派と頻度派の対照表
おわりに

本章は次のような記述からはじまります．

ベイズ派の推論法は頻度主義と真っ向から対立している．というのは言いすぎだとしても，少なくとも直交はしている．
（中略）
2つの哲学の美点を合体させるための苦労は，より込み入ったデータ集合を扱わなければならない現代では，より重大になっている．

いきなり読み進めるのが楽しみになるような文言ですね．「直交する」というのはどのようなことなのか，いろいろ考えてしまいますが，進めていきます．

はじめに

頻度派においてもベイズ派においても，確率密度の族がその根幹にあります．まずはその数式の準備がされています．

標本空間 $\mathcal X$ ，パラメータ空間 $\Omega$ ，密度関数 $f _ \mu(x)$ からなる族を $\mathcal F = \{f _ \mu(x); x\in\mathcal X, \mu\in\Omega\}$ とします． $x, \mu$ はそれぞれ空間内のひとつの値です．この族に加え，ベイズ派ではさらに事前知識の仮定をおきます．つまり $g(\mu),~ \mu\in\Omega$ です．そもそも「事前知識」とはなにか，という率直な疑問についてはさほど触れられておらず，核となるベイズの定理の説明に進みます．どのような場合に事前知識が明らかかは，この章のいくつかの事例を通して触れられています．

ベイズの定理は次式で与えられます．

$\displaystyle g(\mu|x)=\frac{g(\mu)f_\mu(x)}{f(x)}, \mu\in\Omega.$

ベイズの定理や事後分布についての説明は，どの基本的な統計の本にも載っているような事項なので，この記事では割愛します．上式より明らかですが，事後分布で $x$ は観測値に固定されています．一方で， $\mu$ は $\Omega$ に渡って変化する変数として扱っています．これは頻度派とはちょうど逆になっていますね．さらに， $x$ は固定されているので，分母の $f(x)$ は，定数扱いすることができます．事後密度の面積を1にするための正規化定数と捉えることもできます．また，任意の異なるパラメータ $\mu_1, \mu_2\in\Omega$ に対して $f(x)$ は共通しているため，それぞれのもとでの事後密度の比は次のようになります．

$\displaystyle \frac{g(\mu_1|x)}{g(\mu_2|x)} = \frac{g(\mu _ 1)f _ {\mu _ 1}(x)}{g(\mu _ 2)f _ {\mu _ 2}(x)}.$

つまり， $f(x)$ を考えずに両者を比較・評価することができます．この便利な形（事後オッズ比）は，ベイズ流の検定やMCMCのアルゴリズムなどでしばしば利用されている気がします．

3.1 2つの例

まず3.1節では，ベイズ則がどのように使われるか，2つの例を示してその便利さが示されています．

物理学者の双子の例

まず1つ目は，ある物理学者が双子の男の子を身篭っていると知ったとき，その双子が二卵性双生児であるか一卵性双生児であるかを推論する問題です．簡潔に整理してみます．

一卵性では，基本的に同性になります（少し調べてみると，稀に違うときもあるようです）．一方で二卵性では，同性になる確率も異性になる確率も1/2になります．一卵性になるか二卵性になるかのベルヌーイ試行で，パラメータ $\mu$ が異なるイメージです．また，双子が同性であるかどうかも二者択一であるため，こちらもベルヌーイ試行にしたがいます．そこで，同性になるとき1，異性になるとき0になるような確率変数 $X$ を考えます．

$X\sim Belnoulli(\mu), 0\geq\mu\geq1.$

また，上述の事実より，双子が同性になるかどうかの確率を支配する母数 $\mu$ は，双子が一卵性か二卵性かによって異なります．一卵性のときを $\mu_1$ ，二卵性のときを $\mu_2$ としましょう．すると，この問題は，双子が同性である，つまり $X = 1$ を観測したときに， $\mu_1, \mu_2$ の事後確率はそれぞれどれほどになるか，という問題で考えることができます．つまり，次の二つを比較すれば良いことになります．

$g(\mu = \mu_1 | X=1) = \frac{g(\mu = \mu_1)f(X=1|\mu_1)}{f(X=1)}$ .
$g(\mu = \mu_2 | X=1) = \frac{g(\mu = \mu_2)f(X=1|\mu_2)}{f(X=1)}$ .

これらは， $g(\mu)$ が自然の摂理から明らかであること， $f(X=1|\mu_1) = 1$ であることなどを利用すれば求めることができます．本書では前述の事後オッズ比を求めており，「双子の男の子」という観測のもとで両者の事後確率が等しいことを示しています．

この例を整理した図3.1は解析ではないためこの記事で再現はしませんが，これは $X, \mu$ の同時分布を整理したものです． $X$ も $\mu$ も2つの値しか取らないため，このような図で整理することができますが，次元が大きくなったり連続変数になったりするとこのような整理は不可能です．しかし，この図が分かり易くしているような，同時確率と周辺確率，事後確率，事前確率をいったりきたりすることはベイズ派，ひいては頻度派でも超重要と思われます．私が技術書や論文を読むときは数式をさくっと追うだけになってしまいがちなのですが，逃げることなくしっかりやりたいです（自戒）．

テストの点数の例

2つ目の例は，22名の学生に対して実施した2科目のテスト点数の相関係数についての例です．大きさ22の標本から普通にもとめた相関係数は0.498になりますが，ありとあらゆる学生に対して実施したときの相関係数を知りたい，というのは自然な欲求です．

これは後の5章で議論されることですが，2つの科目の点数の同時分布が2変量正規分布に従うとしたとき，その相関係数の分布は次式になります． $\hat\theta$ にはデータから推定した相関係数の値を差し込み (plug-in) ます．

$\displaystyle f _ \theta(\hat \theta) = \frac{(n-2)(1-\theta^{2}) ^ {(n-1)/2}(1-\hat\theta^{2}) ^ {(n-4)/2}}{\pi} \int^\infty_0 \frac{dw}{(\cosh w - \theta\hat\theta)^{n-1}}.$

この例では，事前知識の入れ方として，次の3つの場合を紹介しています．

無情報事前分布
- $g(\theta) = 1/2, ~ -1\geq\theta\geq 1$ .
三角事前分布
- $g(\theta) = 1 - |\theta|$ .
ジェフリーズの事前分布
- $g(\theta) = 1 / (1-\theta^{2})$ .

式より，無情報事前分布は $\theta$ が $\Omega$ にわたり一様に分布している，平坦な分布です．三角事前分布は，0を中心として三角形の形をしている分布です．ジェフリーズの事前分布に関しては知識がないと何が何やら分からないと思うので．次で整理したいと思います．

それでは，事後分布は $g(\theta|\hat\theta) = \frac{g(\theta)f_ \theta (\hat\theta)}{f(\hat\theta)}\propto g(\theta)f _ \theta(\hat\theta)$ で計算できることを思い出し，それぞれの事前分布から計算してみましょう．ここで， $f(\hat\theta) = \int _ {-1} ^ {1} g(\theta)f _ \theta(\hat\theta)d\theta$ は正規化定数とみなせるため，あとで積分して1に調整してしまうことにしていったん放置しましょう．それぞれ計算して，各事前分布を置いたときの事後確率は次のように表せます． $n$ には22を代入してあります．

無情報事前分布の場合

$\displaystyle g _ {flat}(\theta|\hat \theta) \propto \frac{10}{\pi} (1-\theta^{2}) ^ {10.5} (1-\hat\theta^{2}) ^ {9} \int^\infty_0 \frac{dw}{(\cosh w - \theta\hat\theta)^{21}}.$

三角事前分布の場合

$\displaystyle g _ {triangle}(\theta|\hat \theta) \propto \frac{20(1-|\theta|)}{\pi} (1-\theta^{2}) ^ {10.5} (1-\hat\theta^{2}) ^ {9} \int^\infty_0 \frac{dw}{(\cosh w - \theta\hat\theta)^{21}}.$

ジェフリーズの事前分布の場合

$\displaystyle g _ {jeff} (\theta | \hat \theta) \propto \frac{20}{(1-\theta^{2})\pi} (1-\theta^{2}) ^ {10.5} (1-\hat\theta^{2}) ^ {9} \int^\infty_0 \frac{dw}{(\cosh w - \theta\hat\theta)^{21}}.$

図3.2

以上，事後分布がもとまったので，Rで作図していきましょう． tidyverseを読み込み，データをダウンロードします．また，差し込む相関係数の推定値も算出しておきます

library(tidyverse)

scores <- read_delim("https://web.stanford.edu/~hastie/CASI_files/DATA/student_score.txt",
                     delim = " ")

# 相関係数の算出
theta_hat <- cor(scores$mech, scores$vecs)

$w$ の積分の部分はすべてに共通しているため，f_denom()としてわけて考えます．残りの部分はそれぞれf_***_nume()として定義します．ネーミングは雑に「分子」「分母」から取りましたw． f_denom()では数値積分を行う必要があるのですが，ここではひと工夫必要です． Rで数値積分するにはintegrate()を使えば良いのですが， $\theta$ を与えつつ $w$ の関数として扱いたいため，さらに関数を戻り値にしています．

# 共通するwで積分する部分
f_denom <- function(theta){
  return(function(w){1 / (pi * (cosh(w) - theta*theta_hat)^21) })
}

# 無情報事前分布
f_flat_nume <- function(theta){
  10*(1-theta^2)^10.5*(1-theta_hat^2)^9
}

f_flat <- function(theta){
  f_flat_nume(theta) * integrate(f_denom(theta), 0, Inf)$value
}

# 三角事前分布
f_triangle_nume <- function(theta){
  20*(1-abs(theta))*(1-theta^2)^10.5*(1-theta_hat^2)^9
}

f_triangle <- function(theta){
  f_triangle_nume(theta) * integrate(f_denom(theta), 0, Inf)$value
}

# ジェフリーズの事前分布
f_jeff_nume <- function(theta){
  20*(1-theta^2)^9.5*(1-theta_hat^2)^9
}

f_jeff <- function(theta){
  f_jeff_nume(theta) * integrate(f_denom(theta), 0, Inf)$value
}

次に，放置していた正規化定数を計算しましょう．確率密度は面積が1にならなくてはならないので，最後に正規化定数で割らなければなりません．関数を入れ子にしているためか，integrate()ではうまくいかなかったので，重積分も可能なcubature::adaptIntegrate()を使います．必要に応じてインストールinstall.packages("cubature")します．

library(cubature)

norm_const_flat <- adaptIntegrate(f_flat, -1, 1)$integral
norm_const_triangle <- adaptIntegrate(f_triangle, -1, 1)$integral
norm_const_jeff <- adaptIntegrate(f_jeff, -1, 1)$integral

それでは作図します．ggplot2::stat_function()を使おうかとも思ったのですが，面倒だったので作った関数で値を計算して素直にgeom_line()で書きました．また，軸ラベルに数式を書くところではTeX記法を使いたかったので，latex2exp::TeX()を使っています．expression()で頑張っても良いでしょう．これも必要に応じてインストールしてください．

library(latex2exp)
tibble(theta = seq(-1, 1, 0.01)) %>% 
  mutate(p_flat = map_dbl(theta, f_flat) / norm_const_flat,
         p_triangle = map_dbl(theta, f_triangle) / norm_const_triangle,
         p_jeff = map_dbl(theta, f_jeff) / norm_const_jeff) %>% 
  gather(key, p, -theta) %>% 
  ggplot(aes(theta, p, group = key))+
  geom_line(aes(linetype = key))+
  geom_vline(xintercept = theta_hat)+
  scale_x_continuous(limits = c(-0.3, 1))+
  labs(x = TeX('$\\theta$'),
       y = TeX('$g(\\theta | \\hat{\\theta})$'), 
       linetype = "事前分布")

f:id:kur0cky:20200907051435p:plain

無事綺麗な図を書くことができました．

3.2 無情報事前分布

さて，テストの例では，特に2科目の点数の相関について事前知識があるわけではありませんでした．このように，役立つ事前情報に恵まれない場合でも，ベイズ即を使いたいときがあるかもしれません．その一つの方法が無情報事前分布(uninformative prior)です．

無情報事前分布は前節でも使いましたが，事前知識を持たないことを再現したいので，いたるところで一様な分布ということになります．ちなみに，これは多くの人が聞いたことがあると思いますが，無情報事前分布を用いた場合のMAP推定値は，次式のように最尤推定値に等しくなります．読み進めるにつれまた扱う機会があると思います．

$\theta _ {MAP} = \text{arg max} _ {\theta} p(\theta|x) = \text{arg max} _ {\theta}p(x|\theta)p(\theta) = \text{arg max} _ {\theta}p(x | \theta)$

しかし，無情報事前分布には一つ欠陥があります．パラメータ空間が $\Omega = (-\infty, \infty)$ であるとき，無情報事前分布を一様分布としてしまうと $\int _ {-\infty} ^ {\infty} p(\theta) \neq 1$ になってしまうのです．これは確率の公理を満たさず，improper prior distributionとよばれます．

十分広い閉区間に局所一様分布を考えれば問題ないですが，これも変数変換などによって一様性が失われてしまいます．これを解決するための手法に，先ほどもでてきた「ジェフリーズの事前分布」があります．

ジェフリーズの事前分布

初見では理解できないと思ったので簡単に解説を入れることにします．

ジェフリーズの事前分布とは，特定の事前分布のことを指すのではなく，事前分布を構成するための「規則」です．そして，この「規則」とは，「パラメータを変数変換しても事後分布への影響が不変になるように事前分布を選択すること」です．

どうしてそのようになるかの証明は後回しにし，まずはジェフリーズの事前分布の定義を紹介します．

$p _ {jeff}(\theta) \propto \sqrt{\mathcal I_ {\theta}}$ .

ここで， $\mathcal I_ {\theta}$ は $\theta$ のフィッシャー情報量です．つまり，ジェフリーズによる「規則」は，「パラメータのフィッシャー情報量に比例するように事前分布を選ぶ」という規則でもあります．フィッシャー情報量は4章ででてくるのでここでは割愛しますが，簡単に言うと「対数尤度の偏微分（スコア関数）の分散」です．推定量の良さを評価する一手法クラメル・ラオの下限に使われることで知っている人も多いと思います．

詳しく知りたい方は以下の記事などを読むとわかりやすい気がします．

qiita.com

定義を紹介したところで，本当にパラメータの変数変換に対して不変であるのか，示したいと思います．

$\displaystyle \begin{align} p(\phi)\left| \frac{d\phi}{d\theta} \right| & \propto \sqrt{\mathcal I _ \phi \left( \frac{d\phi}{d\theta}\right) ^ 2} \\ & = \sqrt{E\left[\left(\frac{d\log L}{d\phi}\right) ^ 2\right] \left( \frac{d\phi}{d\theta}\right) ^ 2} \\ & = \sqrt{E\left[\left(\frac{d\log L}{d\theta} \right) ^ 2 \right ]} \\ & = \sqrt{\mathcal I _ \theta}. \end{align}$

上の式変形より， $p(\phi) \propto \sqrt{\mathcal I _ \phi}$ から変数変換をしても $p(\theta) \propto \sqrt{\mathcal I _ \theta}$ がいえたので，変数変換に対して不変であるとわかりました．半ばトップダウン的な形で示しましたが，なんだか美しいですね． フィッシャー情報量の平方根に比例さえするように事前分布を選べば，変数変換しても問題ないというわけです．パラメータが複数の場合は行列を考えなければいけないのですが，ここでは割愛します．

3.3 頻度派的な推論の欠陥

この節では，3つの例を通して，頻度派的推論の弱点を指摘しています．

検診員の例

この例に関しては正直よくわかりませんでしたが，なんとか次のように考えました．間違っていたら教えて欲しいです．

まずは次の記述についてです．

次の日，彼は電圧計に不具合を見つけた．電圧が100を超えた場合はすべて $x = 100$ と報告されたかもしれないというのである．頻度派統計学者風に考えると， $\bar x = 92$ は真の期待値 $\mu$ に対してもはや不変ではない．

$\bar x = \frac{1}{n}\sum x$ は，計測値が $x\sim \mathcal N (\mu, 1)$ になるように調整されている，という前提のもとで不偏な推定量であるため，その前提が覆された以上不偏な推定は行えない，ということでしょうか．ここまでは何となく良さそうな気がします．

つづいて次の記述があります．

ベイズ派の統計学者風に考えてみる．任意の事前密度 $g(\mu)$ に対して，12個の計測値からなるベクトル $\bf x$ における事後密度 $g(\mu|{\bf x}) = g(\mu)f _ \mu ({\bf x})/f({\bf x})$ は，実際に観測されたデータ $\bf x$ のみに依存し，「観測されたかもしれない他の潜在的なデータ集合 $X$ 」には依存しない．

これについてはよく分かりませんでした．計測値が正規分布に従うという前提がある以上，尤度 $f _ \mu ({\bf x})$ の計算には正規分布の密度関数を使うことになると思います．その前提が崩れた以上，事後密度が「データ $\bf x$ のみに依存する」からといって， $\bar x = 92$ を事後期待値として報告することには依然として問題がある気がしました．

途中で実験をやめる例

典型的なp-hackingの例です．この例では，実験者が予定していた30回の実験を待たずに，「20回目であわよく有意な結果が得られていれば実験をそこで終わりにしよう」と結果を盗み見てしまいました．そのため，結局30回目で有意になり棄却できたとしても，もはやこの実験の有意水準は元の値ではなくなってしまった，ということになります．はじめから，「20回もしくは30回目のいずれかで有意になったときに実験を停止する」という規則で検定を設計しなければなりません． p-hackingはよくないですね．結果が有意になるまでデータを採り続ける，というのも同様です．

頻度派的な推論ではついこのようなことが出来てしまいますが，ベイズ派では実験が早く中止になったかどうかに関わらず，事後分布を見ればよいため，寛容である．との主張がなされています．．

この例はランダムネスのみに依存して再現不可能なので，割愛します．

prostateデータの例

この例では，前立腺がんの研究に関するデータを扱います． 52人の患者と50人の健常者に対し，6033個の遺伝子について値を測定したデータです．解析例では，すべての遺伝子について，患者と健常者で平均の差の検定を行っています．また，その検定統計量をなぜか標準偏差1の正規分布に従うように変換しています．理由はよくわかっていないのですが，Efron(2010, Section 7.4) を読めば分かるようです．ここでは深く追いません．

https://www.cambridge.org/core/books/largescale-inference/A0B183B0080A92966497F12CE5D12589

まずはデータを読み込みましょう．

prostmat <- read_csv("https://web.stanford.edu/~hastie/CASI_files/DATA/prostmat.csv")
prostz <- scan("https://web.stanford.edu/~hastie/CASI_files/DATA/prostz.txt", 
               what = double())

それでは解析していきます．すべての遺伝子に対して $t$ 検定をしなければならないので，遺伝子ごとにインデックスgene_indexをつけ，nest()し，map()で回すのが早そうですね．また，検定統計量を正規分布に従うように直す作業はqnorm(pt(statistic, df = 100)))でやっています． pt()で自由度100の $t$ 分布における下側確率を求めた後，qnorm()で，その下側確率に対応する正規分布での値を求めています．

prostate_test <- prostmat %>% 
  mutate(gene_index = 1:n()) %>% 
  gather(key, value, -gene_index) %>% 
  mutate(key = str_remove_all(key, "_.*")) %>% 
  group_by(gene_index, key) %>% 
  nest() %>% 
  ungroup() %>% 
  mutate(data = map(data, ~ unname(unlist(.x)))) %>% 
  spread(key, data) %>% 
  mutate(t_test = map2(cancer, control, ~ 
                         t.test(.x, .y, paired = F, var.equal = F)),
         statistic = map_dbl(t_test, ~ .x$statistic),
         x = qnorm(pt(statistic, df = 100)))

print(prostate_test)

出力すると次のようになります．私はnest()とmap()信者なのですが，このように管理できるのはたとえば交差検証やtarget encodingでもめちゃくちゃ便利です．

> print(prostate_test)
# A tibble: 6,033 x 6
   gene_index cancer     control    t_test  statistic       x
        <int> <list>     <list>     <list>      <dbl>   <dbl>
 1          1 <dbl [52]> <dbl [50]> <htest>    1.48    1.47  
 2          2 <dbl [52]> <dbl [50]> <htest>    3.70    3.57  
 3          3 <dbl [52]> <dbl [50]> <htest>   -0.0278 -0.0278
 4          4 <dbl [52]> <dbl [50]> <htest>   -1.14   -1.13  
 5          5 <dbl [52]> <dbl [50]> <htest>   -0.141  -0.140 
 6          6 <dbl [52]> <dbl [50]> <htest>    0.963   0.959 
 7          7 <dbl [52]> <dbl [50]> <htest>    1.07    1.07  
 8          8 <dbl [52]> <dbl [50]> <htest>   -1.30   -1.29  
 9          9 <dbl [52]> <dbl [50]> <htest>   -1.24   -1.23  
10         10 <dbl [52]> <dbl [50]> <htest>    1.18    1.18  
# … with 6,023 more rows

それでは作図してしまいます．

prostate_test %>% 
  ggplot(aes(x))+
  geom_histogram(colour = "gray25", fill = "green",
                 bins = 50)+
  labs(x = "効果量の推定値",
       y = "度数")

f:id:kur0cky:20200909045331p:plain

本書では，遺伝子610が示す最も大きい値5.29をとりあげ，これは過大評価されており，下方修正すべきとしています．「最大値を取る遺伝子をとってくる」という作業をしているので，これは順序統計量と比較しなければならないということでしょうか．この例は15章でまた出てくるらしいので，そのときを楽しみに待つことにします．ちなみに私はまだそこまで読み進められていません笑

3.4 ベイズ派と頻度派の対照表

この節では，頻度派とベイズ派の比較が行われています． 3章まででは具体的な手法がそれほど解説されているわけではないので，抽象的な表現もあります．むしろ読み進めた後に立ち返ると良いのでは，と個人的には思いました．私の実力不足もあり完全には噛み砕けていませんが，ここでは備忘録的に少し整理します．解析はありません．

両主義の比較は，次の文章を起点とし，細かいスタンスの違いや良し悪しを列挙する形で行われていきます．

どちらも式(3.1)の確率分布族 $f_\mu(x)$ から出発しており，いわば最初は同じ場所で仲良く遊んでいたのだが，そのうちに直交した方向に歩み始める．
（中略）
ベイズ推論は垂直方向に，すなわち $x$ を固定した上で事後分布 $g(\mu|x)$ に従って進むが，頻度派の考え方は水平方向である．すなわち， $\mu$ を固定した上で， $x$ を変化させて考える．

ここまで整理してきても何が「直交」なのかいまいち分かってないのですが，結局単純に次のような整理を比較させただけでしょうか．

ベイズ派：得られたデータを所与とし，確率モデルと事前分布の仮定のみで事後分布を推定する．
頻度派：データの背後に一定の確率分布が存在すると仮定し，その着目する性質 $\mu$ と，それを推定する想定するアルゴリズム $t(x)$ で議論する．議論が十分になされた後，選択したアルゴリズムにデータを代入する．

そこからの比較は箇条書き的に行われており，超要約すると次のような感じです．

事前分布が具体的に想定される場合は躊躇せずベイズの定理を使える．そうでない場合はジェフリーズの事前分布のようなテクニックもあるが，論理的一貫性の魅力（？？？）は享受できない．
良さげな事前分布がない場合，どうしても恣意性がつきまとう．頻度派は常に客観性を要求する．
ベイズ派では，一度事前分布を定めてしまえば，（MCMCや変分推論のようなアルゴリズムはさておき）事後分布だけに着目すればよい．頻度派で選択するアルゴリズムは全てそこから計算できる．
一方で頻度派では，頻度派では，事前分布を選ぶ代わりに，注目したい母集団の性質ごとにアルゴリズムを選択し，その確率的性質に関して議論する．異なる問題に対しては異なるアルゴリズムを考える．想定される分布族の元でアルゴリズムの性質を議論し，比較検討しなければならない．そのため，分布とアルゴリズムに対しone-to-oneに設計されるため，場当たり的になる．手始めに無情報事前分布をおいて行うベイズ推論に人気があるのも，ここを避けれることが大きな理由．
事前分布の選択こそベイズの課題．頻度主義はより慎重な姿勢．母数 $\mu$ がどんなものであれ破綻しないように議論する．もしくは特定の状況下であればうまくいく，というような議論が行われる．
動的な更新が必要な状況下ではベイズは魅力的．物事が進展するにつれ確率が更新されていくのは自然だし，共役事前分布などが大活躍する．

しばしば出てくるベイズの「論理的一貫性」という表現について，あまりピンときていません．単に，事前分布と確率モデルから事後分布の推論のみの議論だけで最後までいける，ということでしょうか．

おわりに

3章も無事まとめ終わりましたが，割と広い知識が求められているので良い復習になっています． 4章以降は具体的な論理が展開されていくので，はやく次の記事を出せるようにしたいです．割と時間がかかってしまっています．．．社会人になり，どのように時間を使っていくか，悩ましい限りです．

2020-08-23

「大規模計算時代の統計推論」を全部Rでやってみる ~第2章~

R CASI 大規模計算時代の統計推論

こんにちは，kur0ckyです．最近は辛い料理を作るのにハマっているのですが，そのせいで腸内環境が大変なことになってます．

さて，エフロン＆ヘイスティの「大規模計算時代の統計推論」に載っている解析をすべてRでやってみる，ということをやっていたのでした．前回記事はこちらです．

kur0cky.hatenablog.com

つづく第2章は「頻度派的な推論」というタイトルで，そもそも頻度主義とはなにか，というところから解説されています．本章は解析が少なく内容が軽くなってしまったので，私の知らなかった概念や，少しややこしい概念について補足的なポエムも書いてみました．誤りを見つけたときは石を投げてください．それではやっていきます．

はじめに
2.1 実践における頻度主義
- 不動統計量について
- 表2.1
2.2 頻度派的な最適性
- 統計的仮説検定について
- どのような検定が望ましいか
2.3 補足と詳細
おわりに

例のごとくtidyverseを読み込んでおきます．ggplot2の設定もしておきます．

library(tidyverse)
theme_set(theme_classic(base_family = "HiraKakuPro-W3"))

はじめに

頻度派主義の巨人について

ピアソン，フィッシャー，ネイマンが頻度主義の大家であることは知っていましたが，本書ではホテリングの名前もその一人として挙がっていました．ホテリングは古典的な異常検知で有名なホテリング理論ぐらいしか知らないのですが（無知），時間があればその辺りも調査してみたいです．言われてみればたしかに，データの背後に多次元正規分布を仮定し，分布から遠い（非常にまれな事象）を異常値とみなす，というのはなんだか頻度主義っぽいかもしれません．

腎臓病のデータについて

本章ではまずはじめに，腎臓病検査のgfrという数値を例にあげ，ある統計量の確率的性質をみることの有用性を示しています．

さっそく公式HPからデータをダウンロードしましょう．変数は1つしかなく，レコードが改行で区切られているtxtファイルになっています． readr::read_csv()などでも読むことができますが，ここではbase::scan()を使ってみましょう． scan()はファイルからベクトルを読み込む関数です． read_lines()でも読むことができる（ただしcharacter型になる）ので，そちらの例も合わせてしめしておきます．ちなみに，readr::read_lines_raw()を用いると，エンコーディング前の未加工の状態でテキストを読み込むことができます．エンコーディングが予めわからない場合などに用いると有用でしょう．

gfr <- scan("https://web.stanford.edu/~hastie/CASI_files/DATA/gfr.txt",
            what = double())
# read_lines("https://web.stanford.edu/~hastie/CASI_files/DATA/gfr.txt") %>% 
#   as.integer()

続いて，平均値とその標準誤差を算出します．平均値の標準誤差は，各要素が同一の確率分布から独立に得られていると考えると，以下のように算出することができます．平均値は54.2654，標準誤差は0.9445844となり，は本書の値とも一致しますね．本書ではこれらの数値をもとに，小数点以下の数値が信用に足らないことを指摘しています．

簡単なのでライブラリなどは使うまでもないですが，強いて使うならば，rapportools::se.mean()などがあります．

# 平均値の算出
mean(gfr)
# 標準誤差の算出
sqrt(var(gfr) / length(gfr))
# パッケージを使う例
rapportools::se.mean(gfr)

分布を確認するためにヒストグラムを描きましょう． ggplot2で書くために一旦tibble（data.frame）に直します．本書の図にできるだけ近づけるため，binsも色々ためしてみましたが，結局完璧には合わせられず断念しました笑．

df_gfr <- tibble(gfr)
df_gfr %>% 
  ggplot(aes(gfr))+
  geom_histogram(bins = 30, colour = "black", fill = "green")+
  labs(y = "度数",
       x = "gfr")

f:id:kur0cky:20200823003751p:plain

頻度主義的推論の手続きについて

頻度主義でよく行われる推論について，感覚的な紹介がされています．まず，以下のような数学的対象が導入されます．

$F$ ：データが従う確率分布
$X$ ：理論的標本（確率変数）． $F \rightarrow {\bf X}, {\bf X} = (X _ 1, \dots, X _ n)$
$x$ ：標本の実現値． ${\bf x} = (x _ 1, \dots, x _ n)$
$\theta$ ：確率分布 $F$ の母数（もしくは性質）
$\hat\Theta = t({\bf X})$ ： $\theta$ の理論的な標本．いわゆる推定量．確率的な性質をもつ
$\hat\theta = t(\bf x)$ ：推定量に実際に観測された標本を入れたもの．推定値．単一の値

似たような記号がたくさん出てくるため，腑に落ちるまで少し時間がかかるかもしれません．また， $\hat\Theta$ や $X$ を考える意味も分かりにくいかもしれません．

ただ，上で太字で示したように， $\hat\theta$ や ${\bf x}$ はあくまでも実現した1つの値です．そして，「なんらかの計算アルゴリズム $t$ 」に対し，確率的な性質を考えることこそが重要であるため（確率のことばで議論するため），確率変数や理論的標本を考えるのだと私は整理しています．

2.1 実践における頻度主義

本節では，頻度主義でしばしば行われるいくつかの工夫を通して，「頻度主義とは何か」がフワっと述べられています．

上で触れたように，頻度主義では，ある計算アルゴリズム（たとえば平均など）に対して，その確率的性質を導き出します．このとき，データが従う確率分布 $F$ を知りもしないのに， $F \rightarrow {\bf X}$ を用いた $\hat\Theta = t({\bf X})$ の性質を議論しなくてはなりません．そこで，本書では次の5つの工夫を紹介しています

差し込み法 (plug-in principle)
テイラー級数近似（デルタ法; delta method）
パラメトリック分布族と最尤理論
模擬実験とブートストラップ法
不動統計量 (pivotal statistic)

不動統計量について

上の4つは有名ですし，後の章で詳しく触れられるのでここでは割愛します．しかし，これは私が無知なだけですが，不動統計量というのは初めて聞きました．本書では，不動統計量について以下のように説明し，その例としてスチューデントの2標本 $t$ 検定を紹介しています．

不動統計量 $\hat{\theta} = t(x)$ とは，背後にある確率分布 $F$ に依存しない分布を持つ統計量のことである．

$t$ 検定は標本が正規分布に従うことを仮定するので，背後にある確率分布 $F$ に依存しているじゃないか！！と思ったのですが，読み進めて次のように解釈しました．

2つの標本を $\bf x_1, x_2$ としたとき，検定統計量は次のようになります．

$\displaystyle \begin{align} t = \frac{\bar x_2 - \bar x_1}{\hat{\rm sd}}, \hat{\rm sd} = \hat{\sigma}\left(\frac{1}{n_1}+\frac{1}{n_2}\right)^{1/2} \end{align}$

この統計量は仮定した正規分布の母数 $\sigma$ に依存せず，自由度 $n_1 + n_2$ の $t$ 分布に従います．以上から推察するに，不動統計量とは，「特定の分布（族）を仮定するかさておき，その母数に依存しないように設計された統計量」ということでしょうか．

どなたか詳しい方がいたら教えて下さい．

表2.1

ブートストラップ法の使用例として，gfrデータに対する3つの位置推定値と，その標準誤差を推定するタスクを紹介しています．「位置」推定値には平均値，中央値，ウィンザー化平均値を使用しています．平均であればその標準誤差は陽に求まりますが，他2つに関しては難しいためブートストラップ法で推定することになります．

まずは点推定値を求めます．ウィンザー化平均の条件分岐にはみんな大好きcase_when()を使います．

# 予め第1，第3四分位点を求めておく
q1 <- quantile(gfr, 0.25)
q3 <- quantile(gfr, 0.75)
estimated_value <- df_gfr %>% 
  mutate(winsorized_gfr = case_when(gfr < q1 ~ q1,
                                    gfr > q3 ~ q3,
                                    TRUE ~ gfr)) %>% 
  summarise(mean = mean(gfr),
            median = median(gfr),
            winsorized_mean = mean(winsorized_gfr)) %>% 
  gather(var, estimated_value)

print(estimated_value)

# A tibble: 3 x 2
  var             estimated_value
  <chr>                     <dbl>
1 mean                       54.3
2 median                     52  
3 winsorized_mean            52.8

続いて，中央値とウィンザー化平均の標準誤差をブートストラップ法で求めます．ブートストラップ標準誤差の値が本書と若干ずれてますが，ブートストラップの反復回数が少ないということにしておきましょう．

boot_size = 1000
size = length(gfr)
set.seed(1)
se <- df_gfr %>% 
  sample_n(size = n()*boot_size,
           replace = T) %>% 
  mutate(boot_index = rep(1:boot_size, each = size)) %>% 
  group_by(boot_index) %>% 
  mutate(q1 = quantile(gfr, 0.25),
         q3 = quantile(gfr, 0.75),
        winsorized_gfr = case_when(gfr < q1 ~ q1,
                                    gfr > q3 ~ q3,
                                    TRUE ~ gfr)) %>% 
  summarise(median = median(gfr),
            winsorized_mean = mean(winsorized_gfr)) %>% 
  summarise(median = sd(median),
            winsorized_mean = sd(winsorized_mean)) %>% 
  mutate(mean = sqrt(var(gfr) / size)) %>% 
  gather(var, se)

print(se)

# A tibble: 3 x 2
  var                se
  <chr>           <dbl>
1 median          0.874
2 winsorized_mean 0.905
3 mean            0.945

最後に，点推定値と合わせておしまいです．表示順をslice()で調整したり，mutate_if()とround()を組み合わせて数値型のカラムだけ小数点を丸めたりしています．こういうときに***_all()系や***_at()，***_if()は便利ですね．

se %>% 
  right_join(estimated_value, ., by = "var") %>% 
  slice(c(3, 2, 1)) %>% 
  mutate_if(is.numeric, round, 2) %>% 
  as.data.frame() %>%
  column_to_rownames("var") %>% 
  rename(推定値 = estimated_value,
            標準誤差 = se) %>% 
  knitr::kable()

	推定値	標準誤差
mean	54.27	0.94
winsorized_mean	52.81	0.91
median	52.00	0.87

綺麗な表ができあがりました．それにしても，ウィンザー化平均というものは初めて知りました（無知）．調べてみるとロバスト統計ではしばしば用いられているようです．知らないことだらけです．

2.2 頻度派的な最適性

本節では，頻度主義のメリットを「考えるべきは確率モデル $F$ とアルゴリズム $t$ の選択だけで済むこと」としています．また，より良い $t$ の選択手法の例としてフィッシャー情報量限界 (Fisher information bound) とネイマン=ピアソンの補題 (Neyman-Pearson lemma) を取り上げています．

統計的仮説検定について

これは私の感想ですが，ネイマン=ピアソンの補題をこのページ数で取り上げるのは少し無理がある気がしました．本書は，仮説検定の枠組みをよく知っていることが前提にされている気がします．そこで，理解のために必要だと思われるいくつかの概念について，触りだけ紹介しようと思います．より詳しく知りたい方は宿久先生の特集論文などを読むと良いと思います．

www.jstage.jst.go.jp

ここでは次の概念を紹介します．

仮説検定
第一種の過誤
第二種の過誤
ネイマン=ピアソンの基準
単純仮説
複合仮説
検出力
最強力検定
ネイマン=ピアソンの補題

まず仮説検定についてですが，その手続きをざっくりと書くと，以下のようになります．

観測したデータが帰無仮説のモデルのもとで起こる確率を計算する．
設定した有意水準未満でしか起こらない事象を観測したとき，
帰無仮説の仮定のもとでは，起こっている事象はレアすぎると考える．
つまり，帰無仮説が成り立っていないのでは，と判断する．

もちろん，帰無仮説を否定することはできても，支持はできないことには注意が必要です．ここで，有意水準を閾値として判断を行っているため，判断には一定の誤りが伴うことになります．この誤りを次の2つに分類します．

第一種の過誤：帰無仮説が正しいのに，帰無仮説を棄却してしまう誤り
第二種の過誤：逆に，対立仮説が正しいのに，帰無仮説を棄却しない誤り

一般に，第一種の過誤と第二種の過誤はトレードオフの関係にあります．どのように検定を設計するのがよいでしょうか．

どのような検定が望ましいか

ネイマン=ピアソン基準では，どこまで第一種の過誤を許容できるか，つまり有意水準 $\alpha$ を先に定め，そのもとで第二種の過誤 $\beta$ を最小化します．また，対立仮説が正しいときに，帰無仮説を棄却する確率を検出力といいます．つまり，検出力は $1-\beta$ です．まとめると，ネイマン=ピアソン基準を用いるということは，ある $\alpha$ のもとで $1-\beta$ がより大きい検定を「良い検定」とみなすことです．

有意水準が等しい検定 $t _ 1$ が検定 $t _ 2$ よりも検出力が高いとき， $t _ 1$ は $t _ 2$ よりも強力であるといいます．また，最も検出力が高いように設計された検定を，最強力検定といいます．

そして本題ですが， ネイマン=ピアソンの補題は，帰無仮説と対立仮説が単純仮説のとき，尤度比検定が最強力検定となることを主張しています．

ここで単純仮説とは， $H: \theta = \theta_0$ のように一点からなる仮説です．反対に， $H_0: \theta \neq \theta_0$ や $H: \theta \geq \theta_0$ のような仮説を複合仮説といいます．

2.3 補足と詳細

「頻度主義」という言葉の由来や歴史が書かれています．巨人達による足跡の一端が伺い知れて非常に楽しいです．

おわりに

これを書いている現在ですら本書を読み通せていませんが，値段以上の価値があると思います．おすすめです．

本記事に誤りを見つけたときは是非ご指摘のほどお願いします．石を投げてくださっても構いません．

2020-08-09

「大規模計算時代の統計推論」を全部Rでやってみる ~第1章~

R CASI 大規模計算時代の統計推論

かの有名な「カステラ本」の姉妹編？「大規模計算時代の統計推論―原理と発展―」の和訳が発売されました

大規模計算時代の統計推論: 原理と発展

作者:エフロン,ブラッドレイ,ヘイスティ,トレバー
発売日: 2020/07/30
メディア: 単行本

著者はブラッドリー・エフロン，トレヴァー・ヘイスティという超レジェンド研究者達ですが，訳者にもそうそうたる名前が並んでいます．

せっかく新たなバイブルに出会えたので，この本で行われている解析を全てRでやってみる，ということをやっていきます．解析には随時適当なライブラリを使用し，作図・作表には基本的にggplot2, gtパッケージを使います．tidyverseも可能な限り活用していきます．

今回の記事では第1章「アルゴリズムと推論」の再現をします．

準備
1.1 回帰の例
- fig 1.1
- fig 1.2
- tab 1.1
- fig 1.3
1.2 仮説検定
おわりに

準備

まずは，みんな大好きtidyverseを読み込み，ggplot2で日本語フォントが使えるように設定しておきます．

library(tidyverse)
theme_set(theme_classic(base_family = "HiraKakuPro-W3"))

1.1 回帰の例

本節では，157人の被験者について調査された腎機能のデータを用いた分析が示されています．データは2変量であり，ひとつは目的変数である腎機能の健全度tot，もうひとつは説明変数である年齢ageです．

データは公式サイトに上がっているので，tidyverseにも含まれているreadrパッケージで読み込みます． urlに飛べばわかるのですが，元ファイルがスペース区切りなのでread_delim()でdelim = " "を指定します．

kidney <- read_delim(
  file = "https://web.stanford.edu/~hastie/CASI_files/DATA/kidney.txt",
  delim = " ",
  col_types = "dd")
head(kidney)

# A tibble: 6 x 2
    age   tot
  <dbl> <dbl>
1    18  2.44
2    19  3.86
3    19 -1.22
4    20  2.3 
5    21  0.98
6    21 -0.5

fig 1.1

それでは分析を行っていきます．ここでは2つの作業が行われています．

totをageで線形回帰し，回帰直線を求める．
20歳から80歳まで，10歳おきに予測値の標準誤差を求め，エラーバーを追加する．

とりあえず線形回帰し，切片と傾きを得ましょう．

fit_lm_kidney <- lm(tot ~ age, data = kidney)
beta0 <- fit_lm_kidney$coefficients[1]
beta1 <- fit_lm_kidney$coefficients[2]

続いて予測値の標準誤差を求めます．
これはあまり知られていないかもしれませんが，lm()で出力されるモデルでは，predict()のなかでse.fit = TRUEとしてやることで，説明変数の各値での標準誤差を計算することができます．

予めage = 20, 30, ..., 80のデータフレームを作っておき，それぞれに対する予測値，標準誤差を求めましょう．

ages <- tibble(age = seq(20, 80, 10))
df = predict(fit_lm_kidney, ages, se.fit = TRUE) %>% 
  data.frame() %>% 
  bind_cols(ages) %>% 
  select(age, 
         fit_lm = fit,
         se_lm = se.fit)
print(df)

  age     fit_lm     se_lm
1  20  1.2882585 0.2066481
2  30  0.5023743 0.1549648
3  40 -0.2835098 0.1473983
4  50 -1.0693940 0.1893143
5  60 -1.8552781 0.2575947
6  70 -2.6411623 0.3365586
7  80 -3.4270465 0.4202260

結果が出たので，図を作成します．

ageとtotの散布図の上に，先ほど求めた回帰係数で直線を引き，さらにエラーバーを描きます．エラーバーはgeom_segment()で線分を描きますが，本書では標準誤差の±2倍の長さで引いているらしいので，そのようにします．

できるだけ元の図を再現するため，いろいろなオプションを追加しています．

p <- kidney %>% 
  ggplot(aes(age, tot))+
  geom_point(colour = "steelblue", shape = 8)+
  geom_abline(intercept = beta0, slope = beta1, colour = "red")+
  geom_segment(data = df,
               aes(x = age, xend = age,
                   y = fit_lm - 2*se_lm, yend = fit_lm + 2*se_lm))+
  labs(x = "年齢", y = "複合尺度tot")

f:id:kur0cky:20200806000055p:plain

fig 1.2

次は，lowess (locally weighted scatterplot smoother)という手法を用いた平滑化曲線の推定が行われています．線形回帰と異なり，lowessでは標準誤差を陽に表すことができません．そこで，反復計算で推論を行うブートストラップ法で計算することになります．

lowessのアルゴリズムの詳細については割愛しますが，詳しくはwikipediaなどを見てください． en.wikipedia.org

Rにはstats::lowess()があるので，早速実行していきましょう．本書にあるとおりlowess(x, y, 1/3)を実行してみます．

lowess(x = kidney$age,
       y = kidney$tot,
       f = 1/3)

$x
[1] 18 19 19 20 21 21 ...

$y
[1] 1.338870 1.239242 1.239242 1.145344 1.057087 1.057087 ...

これはまずいですね．入力に対する回帰結果だけが返ってきています．10歳ごとのエラーバーが欲しいのに，データに存在しない40歳や50歳の標準誤差を得ることができません．

方針を変え，loess(locally estimated scatterplot smoother) でできる限り同じように解析したいと思います．loessについてもアルゴリズムの詳細は上記リンクなどをご覧ください．

まずは，データを全て使い曲線を推定します．回帰値もさきほどのdfに追加しておきましょう

fit_loess_kidney <- loess(tot ~ age, kidney, 
                          span = 1/3, 
                          degree = 1,
                          family = "symmetric")
df <- df %>% 
  mutate(fit_loess = predict(fit_loess_kidney, age))

続いてブートストラップ法を用いて標準誤差を推定します．
ブートストラップ法では，重複ありで同じ大きさのサンプルを抽出し，複製されたサンプルに対し推定を行います．この作業を大量に行うことにより，推定値自体の経験分布を得ます．

今回は，ブートストラップの反復回数は1000回で行いました．
ブートストラップ法にはbootパッケージという便利なものもあるのですが，今回は簡単な処理なのでforループで書いてしまいます．

result_boot <- tibble() # 空のdata.frameを用意しておく

for(i in 1:1000){
  # ブートストラップサンプルの抽出
  kidney_boot <- kidney %>% 
    sample_n(size = n(), # 同じ大きさ
             replace = T) # 重複あり

  # 抽出したブートストラップサンプルに対し曲線を推定
  fit_boot <- loess(tot ~ age, 
                    data = kidney_boot, 
                    span = 1/3,
                    degree = 1,
                    family = "symmetric")

  # 10, 20, ..., 80歳で当てはめた値を計算
  result_boot <- ages %>% 
    mutate(fit_loess_boot = predict(fit_boot, ages)) %>% 
    bind_rows(result_boot, .)
}

それでは，ブートストラップ標準誤差を計算し，結果に追加します

df <- result_boot %>% 
  group_by(age) %>% 
  summarise(se_loess = sd(fit_loess_boot, na.rm = T)) %>% 
  left_join(df,., by = "age")

これで念願の図を書くことができます！！

kidney %>% 
  ggplot(aes(age, tot))+
  geom_point(colour = "steelblue", shape = 8)+
  geom_line(data = kidney %>% 
              mutate(fit_loess = predict(fit_loess_kidney)),
            aes(y = fit_loess),
            colour = "red")+
  geom_segment(data = df,
               aes(x = age, xend = age,
                   y = fit_loess - 2*se_loess, yend = fit_loess + 2*se_loess))+
  labs(x = "年齢", y = "複合尺度tot")

f:id:kur0cky:20200809203756p:plain

10歳ごとにエラーバーを引かなければいけなかったので少々面倒くさい作業になってしまいました．
脳死な平滑化で良ければ以下のコードで一発だったのですけれどね．笑

kidney %>% 
  ggplot(aes(age, tot))+
  geom_point()+
  geom_smooth(method = "loess", span = 1/3)

f:id:kur0cky:20200809222520p:plain

tab 1.1

ここまできたら結果はdfにまとまっているので，サクッと表にしてしまいましょう．
そこまで込み入った表ではないのでgt は使わず，knitr::kable()で出力してしまいます．

df %>% 
  rename(線形回帰 = fit_lm,
         標準誤差 = se_lm,
         loess = fit_loess,
         ブートストラップ標準誤差 = se_loess) %>% 
  gather(key, value, -age) %>% 
  spread(age, value) %>% 
  rename(age = key) %>% 
  slice(c(3, 4, 1, 2)) %>% 
  mutate_if(is.numeric, round, 2) %>% 
  knitr::kable(format = "html")

age	20	30	40	50	60	70	80
線形回帰	1.29	0.50	-0.28	-1.07	-1.86	-2.64	-3.43
標準誤差	0.21	0.15	0.15	0.19	0.26	0.34	0.42
loess	1.65	0.65	-0.61	-1.24	-1.92	-2.68	-3.49
ブートストラップ標準誤差	0.67	0.24	0.36	0.35	0.37	0.49	0.67

fig 1.3

上で行ったブートストラップ推定のうち，はじめの25個を図示します．また，全データを用いたのものも合わせて示します．
飽きてきて若干コード汚くなってきてますがご容赦ください

result_boot <- tibble()
for(i in 1:25){
  kidney_boot <- kidney %>% 
    sample_n(size = n(),
             replace = T)
  fit_boot <- loess(tot ~ age,
                    data = kidney_boot,
                    span = 1/3,
                    degree = 1,
                    family = "symmetric")
  result_boot <- kidney_boot %>% 
    mutate(fit_loess = predict(fit_boot),
           iter = i) %>% 
    bind_rows(result_boot,.)
}

result_boot %>% 
  ggplot(aes(age, fit_loess, colour = factor(iter)))+
  geom_line(linetype = "dashed", size = .3)+
  geom_line(data = kidney %>% 
              mutate(fit_loess = predict(fit_loess_kidney)),
            aes(y = fit_loess),
            colour = "black", 
            size = 1)+
  theme(legend.position = "none")+
  labs(x = "年齢", y = "複合尺度tot")

f:id:kur0cky:20200809211721p:plain

1.2 仮説検定

2つ目の例では，72名の白血病患者について，7128個の遺伝子群について調べたデータを扱っています．データには2種類の白血病が混ざっており，47名はALL，25名はAMLの患者です．まずはデータを手に入れましょう．飽きてきたので整形もやってしまいます．

leukemia_big <- read.csv("http://web.stanford.edu/~hastie/CASI_files/DATA/leukemia_big.csv")

gene136AML <- leukemia_big %>% 
  select(starts_with("AML")) %>% 
  slice(136) %>% 
  unlist() %>% 
  unname()
gene136ALL <- leukemia_big %>% 
  select(starts_with("ALL")) %>% 
  slice(136) %>% 
  unlist() %>% 
  unname()

fig 1.4

7128個の遺伝子のうち，136番目のものの値をALL, AMLそれぞれでヒストグラムにします．

tibble(x = c(gene136AML, gene136ALL),
       type = rep(c("AML", "ALL"), 
                  times = c(length(gene136AML), length(gene136ALL)))) %>% 
  ggplot(aes(x))+
  geom_histogram(bins = 11, colour="black", fill = "steelblue")+
  facet_wrap(~type,
             ncol = 1)

f:id:kur0cky:20200809213716p:plain

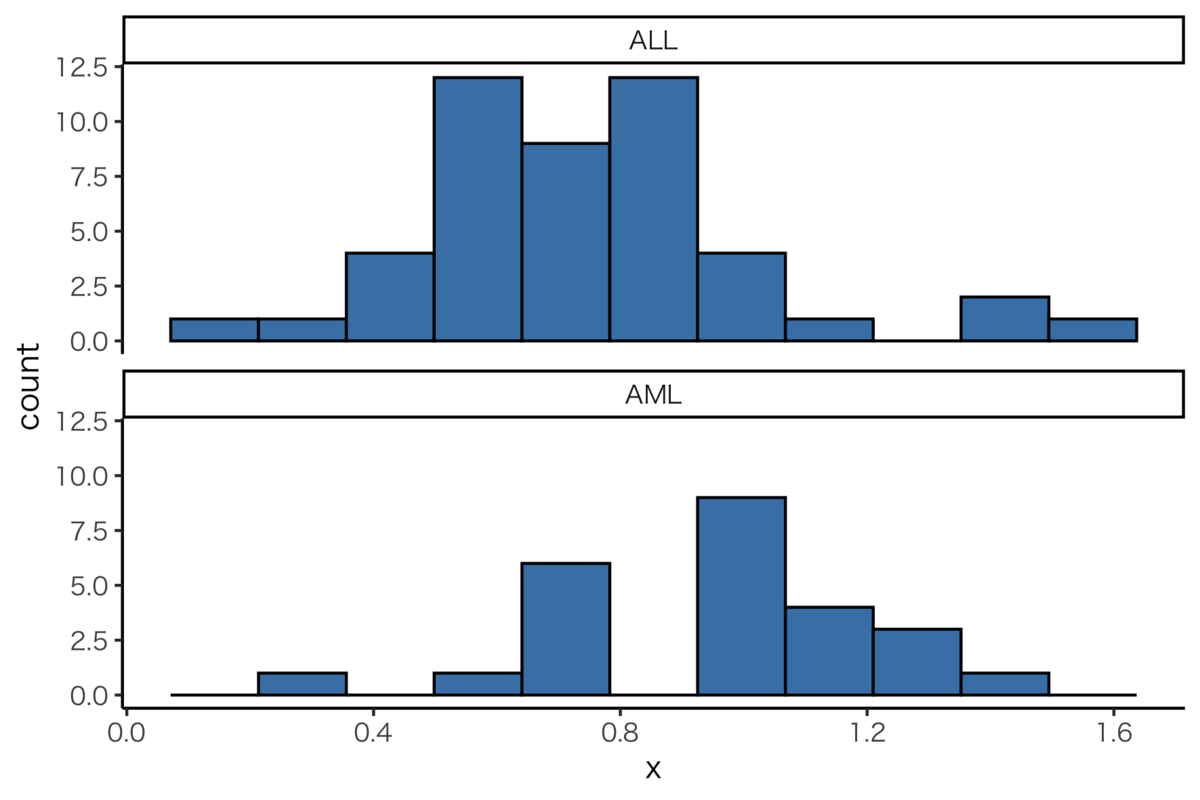
2標本t検定

遺伝子136の平均は，ALLとAMLでそれぞれ0.75, 0.95です．
この2つの分布の平均は異なっていると言えるかどうか，t検定を行います．

> mean(gene136ALL)
[1] 0.7524794

> mean(gene136AML)
[1] 0.9499731

> t.test(gene136AML, gene136ALL, var.equal = T)

    Two Sample t-test

data:  gene136AML and gene136ALL
t = 3.014, df = 70, p-value = 0.003589
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 0.06680742 0.32817995
sample estimates:
mean of x mean of y 
0.9499731 0.7524794

結果はp-value = 0.003589となり，本書と同様の値を出すことができました．

「もし本当になにの違いも無ければ，非常にレアな事象が起こっている」ということになります

fig 1.5

最後に図1.5です．

全7128個の遺伝子に対して同様のt検定を行い，自由度70のt分布と比較してみます．
つまり7128回のt検定を行わなくてはならないのですが，ただ単にforループするだけではつまらないので，ここではtidyr::nest()とpurrr:map()を使い，オシャレに解析を管理する方法を共有したいと思います．

nest()した段階で一度出力を見てみます

> df <- leukemia_big %>% 
+   rownames_to_column("gene_index") %>% # 遺伝子番号を示す行名をカラムへ
+   gather(type, value, -gene_index) %>% # カラム名でALL, AMLを切り分けたいので縦長形式に
+   mutate(type = str_sub(type, 1, 3)) %>% # stringrパッケージを活用し，病種を抽出
+   group_by(gene_index, type) %>% 
+   nest()
> print(df)

# A tibble: 14,256 x 3
# Groups:   gene_index, type [14,256]
   gene_index type  data             
   <chr>      <chr> <list>           
 1 1          ALL   <tibble [47 × 1]>
 2 2          ALL   <tibble [47 × 1]>
 3 3          ALL   <tibble [47 × 1]>
 4 4          ALL   <tibble [47 × 1]>
 5 5          ALL   <tibble [47 × 1]>
 6 6          ALL   <tibble [47 × 1]>
 7 7          ALL   <tibble [47 × 1]>
 8 8          ALL   <tibble [47 × 1]>
 9 9          ALL   <tibble [47 × 1]>
10 10         ALL   <tibble [47 × 1]>
# … with 14,246 more rows

nest()で生まれた新たなdataカラムの各要素には，47 × 1のtibbleが格納されていることがわかります！
このように，tibbleはリストを持つことができるのです．

つまりあとは，spread()で横長形式に戻し，t検定を各レコードに対して実行してやれば良いことになるのです．

レコードごとに処理を行いたいので，purrr::map()を活用します．map2()は，2つの同じ長さのリストを利用した処理を行うための関数です．

> df <- df %>% 
+   spread(type, data) %>% 
+   mutate(t_test = map2(AML, ALL, ~ t.test(unlist(.x), unlist(.y))))
> print(df)

# A tibble: 7,128 x 4
# Groups:   gene_index [7,128]
   gene_index ALL               AML               t_test 
   <chr>      <list>            <list>            <list> 
 1 1          <tibble [47 × 1]> <tibble [25 × 1]> <htest>
 2 10         <tibble [47 × 1]> <tibble [25 × 1]> <htest>
 3 100        <tibble [47 × 1]> <tibble [25 × 1]> <htest>
 4 1000       <tibble [47 × 1]> <tibble [25 × 1]> <htest>
 5 1001       <tibble [47 × 1]> <tibble [25 × 1]> <htest>
 6 1002       <tibble [47 × 1]> <tibble [25 × 1]> <htest>
 7 1003       <tibble [47 × 1]> <tibble [25 × 1]> <htest>
 8 1004       <tibble [47 × 1]> <tibble [25 × 1]> <htest>
 9 1005       <tibble [47 × 1]> <tibble [25 × 1]> <htest>
10 1006       <tibble [47 × 1]> <tibble [25 × 1]> <htest>
# … with 7,118 more rows

このような形にしたことで，それぞれ遺伝子に対応する結果を同じレコードで管理できます．
tidyverse，おそろしいですねぇ

それでは最後に，作図して終えたいと思います．

dens = tibble(x = seq(-10, 10, length.out = 1000)) %>% 
  mutate(dens = dt(x, df = 70))
df %>% 
  mutate(p = map_dbl(t_test, ~ .x$statistic)) %>% 
  ggplot(aes(p))+
  geom_histogram(bins = 70, colour = "black", fill = "green")+
  geom_line(aes(x = x, y = dens*3500), data = dens)+
  scale_y_continuous(limits = c(0, 700))+
  labs(x = "t統計量", y = "度数")

f:id:kur0cky:20200806000109p:plain

おわりに

少ないはずの1章から，結構な量になってしまいました．．．若干飽き始めてますが，最後までやりきりたいと思います．

本書については私はまだ読み途中ですが，歴史的敬意や，主義的な対立を踏まえた俯瞰など，「お気持ち」が込められておりニヤニヤしながら読んでいます．

特に，ブートストラップ法への愛がにじみ出ている気がします．